Obtuse triangle formed by the side and diagonals of a regular heptagon
Shorter diagonals
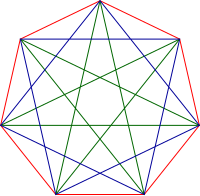
Each of the fourteen congruent heptagonal triangles has one green side, one blue side, and one red side. In Euclidean geometry , a heptagonal triangle is an obtuse , scalene triangle whose vertices coincide with the first, second, and fourth vertices of a regular heptagon (from an arbitrary starting vertex). Thus its sides coincide with one side and the adjacent shorter and longer diagonals of the regular heptagon. All heptagonal triangles are similar (have the same shape), and so they are collectively known as the heptagonal triangle. Its angles have measures
π
/
7
,
2
π
/
7
,
{\displaystyle \pi /7,2\pi /7,}
4
π
/
7
,
{\displaystyle 4\pi /7,}
Key points [ edit ] The heptagonal triangle's nine-point center is also its first Brocard point .[1] : Propos. 12
The second Brocard point lies on the nine-point circle.[2] : p. 19
The circumcenter and the Fermat points of a heptagonal triangle form an equilateral triangle .[1] : Thm. 22
The distance between the circumcenter O and the orthocenter H is given by[2] : p. 19
O
H
=
R
2
,
{\displaystyle OH=R{\sqrt {2}},}
where R is the circumradius . The squared distance from the incenter I to the orthocenter is[2] : p. 19
I
H
2
=
R
2
+
4
r
2
2
,
{\displaystyle IH^{2}={\frac {R^{2}+4r^{2}}{2}},}
where r is the inradius .
The two tangents from the orthocenter to the circumcircle are mutually perpendicular .[2] : p. 19
Relations of distances [ edit ] The heptagonal triangle's sides a < b < c coincide respectively with the regular heptagon's side, shorter diagonal, and longer diagonal. They satisfy[3] : Lemma 1
a
2
=
c
(
c
−
b
)
,
b
2
=
a
(
c
+
a
)
,
c
2
=
b
(
a
+
b
)
,
1
a
=
1
b
+
1
c
{\displaystyle {\begin{aligned}a^{2}&=c(c-b),\\[5pt]b^{2}&=a(c+a),\\[5pt]c^{2}&=b(a+b),\\[5pt]{\frac {1}{a}}&={\frac {1}{b}}+{\frac {1}{c}}\end{aligned}}}
(the latter[2] : p. 13 optic equation ) and hence
a
b
+
a
c
=
b
c
,
{\displaystyle ab+ac=bc,}
and[3] : Coro. 2
b
3
+
2
b
2
c
−
b
c
2
−
c
3
=
0
,
{\displaystyle b^{3}+2b^{2}c-bc^{2}-c^{3}=0,}
c
3
−
2
c
2
a
−
c
a
2
+
a
3
=
0
,
{\displaystyle c^{3}-2c^{2}a-ca^{2}+a^{3}=0,}
a
3
−
2
a
2
b
−
a
b
2
+
b
3
=
0.
{\displaystyle a^{3}-2a^{2}b-ab^{2}+b^{3}=0.}
Thus –b /c , c /a , and a /b all satisfy the cubic equation
t
3
−
2
t
2
−
t
+
1
=
0.
{\displaystyle t^{3}-2t^{2}-t+1=0.}
However, no algebraic expressions with purely real terms exist for the solutions of this equation, because it is an example of casus irreducibilis .
The approximate relation of the sides is
b
≈
1.80193
⋅
a
,
c
≈
2.24698
⋅
a
.
{\displaystyle b\approx 1.80193\cdot a,\qquad c\approx 2.24698\cdot a.}
We also have[4] [5]
a
2
b
c
,
−
b
2
c
a
,
−
c
2
a
b
{\displaystyle {\frac {a^{2}}{bc}},\quad -{\frac {b^{2}}{ca}},\quad -{\frac {c^{2}}{ab}}}
satisfy the cubic equation
t
3
+
4
t
2
+
3
t
−
1
=
0.
{\displaystyle t^{3}+4t^{2}+3t-1=0.}
We also have[4]
a
3
b
c
2
,
−
b
3
c
a
2
,
c
3
a
b
2
{\displaystyle {\frac {a^{3}}{bc^{2}}},\quad -{\frac {b^{3}}{ca^{2}}},\quad {\frac {c^{3}}{ab^{2}}}}
satisfy the cubic equation
t
3
−
t
2
−
9
t
+
1
=
0.
{\displaystyle t^{3}-t^{2}-9t+1=0.}
We also have[4]
a
3
b
2
c
,
b
3
c
2
a
,
−
c
3
a
2
b
{\displaystyle {\frac {a^{3}}{b^{2}c}},\quad {\frac {b^{3}}{c^{2}a}},\quad -{\frac {c^{3}}{a^{2}b}}}
satisfy the cubic equation
t
3
+
5
t
2
−
8
t
+
1
=
0.
{\displaystyle t^{3}+5t^{2}-8t+1=0.}
We also have[2] : p. 14
b
2
−
a
2
=
a
c
,
{\displaystyle b^{2}-a^{2}=ac,}
c
2
−
b
2
=
a
b
,
{\displaystyle c^{2}-b^{2}=ab,}
a
2
−
c
2
=
−
b
c
,
{\displaystyle a^{2}-c^{2}=-bc,}
and[2] : p. 15
b
2
a
2
+
c
2
b
2
+
a
2
c
2
=
5.
{\displaystyle {\frac {b^{2}}{a^{2}}}+{\frac {c^{2}}{b^{2}}}+{\frac {a^{2}}{c^{2}}}=5.}
We also have[4]
a
b
−
b
c
+
c
a
=
0
,
{\displaystyle ab-bc+ca=0,}
a
3
b
−
b
3
c
+
c
3
a
=
0
,
{\displaystyle a^{3}b-b^{3}c+c^{3}a=0,}
a
4
b
+
b
4
c
−
c
4
a
=
0
,
{\displaystyle a^{4}b+b^{4}c-c^{4}a=0,}
a
11
b
3
−
b
11
c
3
+
c
11
a
3
=
0.
{\displaystyle a^{11}b^{3}-b^{11}c^{3}+c^{11}a^{3}=0.}
There are no other (m, n ), m, n > 0, m, n < 2000 such that[citation needed
a
m
b
n
±
b
m
c
n
±
c
m
a
n
=
0.
{\displaystyle a^{m}b^{n}\pm b^{m}c^{n}\pm c^{m}a^{n}=0.}
Altitudes [ edit ] The altitudes h a h b h c
h
a
=
h
b
+
h
c
{\displaystyle h_{a}=h_{b}+h_{c}}
[2] : p. 13 and
h
a
2
+
h
b
2
+
h
c
2
=
a
2
+
b
2
+
c
2
2
.
{\displaystyle h_{a}^{2}+h_{b}^{2}+h_{c}^{2}={\frac {a^{2}+b^{2}+c^{2}}{2}}.}
[2] : p. 14 The altitude from side b (opposite angle B ) is half the internal angle bisector
w
A
{\displaystyle w_{A}}
A :[2] : p. 19
2
h
b
=
w
A
.
{\displaystyle 2h_{b}=w_{A}.}
Here angle A is the smallest angle, and B is the second smallest.
Internal angle bisectors [ edit ] We have these properties of the internal angle bisectors
w
A
,
w
B
,
{\displaystyle w_{A},w_{B},}
w
C
{\displaystyle w_{C}}
A, B , and C respectively:[2] : p. 16
w
A
=
b
+
c
,
{\displaystyle w_{A}=b+c,}
w
B
=
c
−
a
,
{\displaystyle w_{B}=c-a,}
w
C
=
b
−
a
.
{\displaystyle w_{C}=b-a.}
Circumradius, inradius, and exradius [ edit ] The triangle's area is[6]
A
=
7
4
R
2
,
{\displaystyle A={\frac {\sqrt {7}}{4}}R^{2},}
where R is the triangle's circumradius .
We have[2] : p. 12
a
2
+
b
2
+
c
2
=
7
R
2
.
{\displaystyle a^{2}+b^{2}+c^{2}=7R^{2}.}
We also have[7]
a
4
+
b
4
+
c
4
=
21
R
4
.
{\displaystyle a^{4}+b^{4}+c^{4}=21R^{4}.}
a
6
+
b
6
+
c
6
=
70
R
6
.
{\displaystyle a^{6}+b^{6}+c^{6}=70R^{6}.}
The ratio r /R of the inradius to the circumradius is the positive solution of the cubic equation[6]
8
x
3
+
28
x
2
+
14
x
−
7
=
0.
{\displaystyle 8x^{3}+28x^{2}+14x-7=0.}
In addition,[2] : p. 15
1
a
2
+
1
b
2
+
1
c
2
=
2
R
2
.
{\displaystyle {\frac {1}{a^{2}}}+{\frac {1}{b^{2}}}+{\frac {1}{c^{2}}}={\frac {2}{R^{2}}}.}
We also have[7]
1
a
4
+
1
b
4
+
1
c
4
=
2
R
4
.
{\displaystyle {\frac {1}{a^{4}}}+{\frac {1}{b^{4}}}+{\frac {1}{c^{4}}}={\frac {2}{R^{4}}}.}
1
a
6
+
1
b
6
+
1
c
6
=
17
7
R
6
.
{\displaystyle {\frac {1}{a^{6}}}+{\frac {1}{b^{6}}}+{\frac {1}{c^{6}}}={\frac {17}{7R^{6}}}.}
In general for all integer n ,
a
2
n
+
b
2
n
+
c
2
n
=
g
(
n
)
(
2
R
)
2
n
{\displaystyle a^{2n}+b^{2n}+c^{2n}=g(n)(2R)^{2n}}
where
g
(
−
1
)
=
8
,
g
(
0
)
=
3
,
g
(
1
)
=
7
{\displaystyle g(-1)=8,\quad g(0)=3,\quad g(1)=7}
and
g
(
n
)
=
7
g
(
n
−
1
)
−
14
g
(
n
−
2
)
+
7
g
(
n
−
3
)
.
{\displaystyle g(n)=7g(n-1)-14g(n-2)+7g(n-3).}
We also have[7]
2
b
2
−
a
2
=
7
b
R
,
2
c
2
−
b
2
=
7
c
R
,
2
a
2
−
c
2
=
−
7
a
R
.
{\displaystyle 2b^{2}-a^{2}={\sqrt {7}}bR,\quad 2c^{2}-b^{2}={\sqrt {7}}cR,\quad 2a^{2}-c^{2}=-{\sqrt {7}}aR.}
We also have[4]
a
3
c
+
b
3
a
−
c
3
b
=
−
7
R
4
,
{\displaystyle a^{3}c+b^{3}a-c^{3}b=-7R^{4},}
a
4
c
−
b
4
a
+
c
4
b
=
7
7
R
5
,
{\displaystyle a^{4}c-b^{4}a+c^{4}b=7{\sqrt {7}}R^{5},}
a
11
c
3
+
b
11
a
3
−
c
11
b
3
=
−
7
3
17
R
14
.
{\displaystyle a^{11}c^{3}+b^{11}a^{3}-c^{11}b^{3}=-7^{3}17R^{14}.}
The exradius r a a equals the radius of the nine-point circle of the heptagonal triangle.[2] : p. 15
Orthic triangle [ edit ] The heptagonal triangle's orthic triangle , with vertices at the feet of the altitudes , is similar to the heptagonal triangle, with similarity ratio 1:2. The heptagonal triangle is the only obtuse triangle that is similar to its orthic triangle (the equilateral triangle being the only acute one).[2] : pp. 12–13
Trigonometric properties [ edit ] Trigonometric identities [ edit ] The various trigonometric identities associated with the heptagonal triangle include these:[2] : pp. 13–14 [6] [7]
A
=
π
7
cos
A
=
b
2
a
B
=
2
π
7
cos
B
=
c
2
b
C
=
4
π
7
cos
C
=
−
a
2
c
{\displaystyle {\begin{aligned}A&={\frac {\pi }{7}}\\[6pt]\cos A&={\frac {b}{2a}}\end{aligned}}\quad {\begin{aligned}B&={\frac {2\pi }{7}}\\[6pt]\cos B&={\frac {c}{2b}}\end{aligned}}\quad {\begin{aligned}C&={\frac {4\pi }{7}}\\[6pt]\cos C&=-{\frac {a}{2c}}\end{aligned}}}
[4] : Proposition 10
sin
A
×
sin
B
×
sin
C
=
7
8
sin
A
−
sin
B
−
sin
C
=
−
7
2
cos
A
×
cos
B
×
cos
C
=
−
1
8
tan
A
×
tan
B
×
tan
C
=
−
7
tan
A
+
tan
B
+
tan
C
=
−
7
cot
A
+
cot
B
+
cot
C
=
7
sin
2
A
×
sin
2
B
×
sin
2
C
=
7
64
sin
2
A
+
sin
2
B
+
sin
2
C
=
7
4
cos
2
A
+
cos
2
B
+
cos
2
C
=
5
4
tan
2
A
+
tan
2
B
+
tan
2
C
=
21
sec
2
A
+
sec
2
B
+
sec
2
C
=
24
csc
2
A
+
csc
2
B
+
csc
2
C
=
8
cot
2
A
+
cot
2
B
+
cot
2
C
=
5
sin
4
A
+
sin
4
B
+
sin
4
C
=
21
16
cos
4
A
+
cos
4
B
+
cos
4
C
=
13
16
sec
4
A
+
sec
4
B
+
sec
4
C
=
416
csc
4
A
+
csc
4
B
+
csc
4
C
=
32
{\displaystyle {\begin{array}{rcccccl}\sin A\!&\!\times \!&\!\sin B\!&\!\times \!&\!\sin C\!&\!=\!&\!{\frac {\sqrt {7}}{8}}\\[2pt]\sin A\!&\!-\!&\!\sin B\!&\!-\!&\!\sin C\!&\!=\!&\!-{\frac {\sqrt {7}}{2}}\\[2pt]\cos A\!&\!\times \!&\!\cos B\!&\!\times \!&\!\cos C\!&\!=\!&\!-{\frac {1}{8}}\\[2pt]\tan A\!&\!\times \!&\!\tan B\!&\!\times \!&\!\tan C\!&\!=\!&\!-{\sqrt {7}}\\[2pt]\tan A\!&\!+\!&\!\tan B\!&\!+\!&\!\tan C\!&\!=\!&\!-{\sqrt {7}}\\[2pt]\cot A\!&\!+\!&\!\cot B\!&\!+\!&\!\cot C\!&\!=\!&\!{\sqrt {7}}\\[8pt]\sin ^{2}\!A\!&\!\times \!&\!\sin ^{2}\!B\!&\!\times \!&\!\sin ^{2}\!C\!&\!=\!&\!{\frac {7}{64}}\\[2pt]\sin ^{2}\!A\!&\!+\!&\!\sin ^{2}\!B\!&\!+\!&\!\sin ^{2}\!C\!&\!=\!&\!{\frac {7}{4}}\\[2pt]\cos ^{2}\!A\!&\!+\!&\!\cos ^{2}\!B\!&\!+\!&\!\cos ^{2}\!C\!&\!=\!&\!{\frac {5}{4}}\\[2pt]\tan ^{2}\!A\!&\!+\!&\!\tan ^{2}\!B\!&\!+\!&\!\tan ^{2}\!C\!&\!=\!&\!21\\[2pt]\sec ^{2}\!A\!&\!+\!&\!\sec ^{2}\!B\!&\!+\!&\!\sec ^{2}\!C\!&\!=\!&\!24\\[2pt]\csc ^{2}\!A\!&\!+\!&\!\csc ^{2}\!B\!&\!+\!&\!\csc ^{2}\!C\!&\!=\!&\!8\\[2pt]\cot ^{2}\!A\!&\!+\!&\!\cot ^{2}\!B\!&\!+\!&\!\cot ^{2}\!C\!&\!=\!&\!5\\[8pt]\sin ^{4}\!A\!&\!+\!&\!\sin ^{4}\!B\!&\!+\!&\!\sin ^{4}\!C\!&\!=\!&\!{\frac {21}{16}}\\[2pt]\cos ^{4}\!A\!&\!+\!&\!\cos ^{4}\!B\!&\!+\!&\!\cos ^{4}\!C\!&\!=\!&\!{\frac {13}{16}}\\[2pt]\sec ^{4}\!A\!&\!+\!&\!\sec ^{4}\!B\!&\!+\!&\!\sec ^{4}\!C\!&\!=\!&\!416\\[2pt]\csc ^{4}\!A\!&\!+\!&\!\csc ^{4}\!B\!&\!+\!&\!\csc ^{4}\!C\!&\!=\!&\!32\\[8pt]\end{array}}}
tan
A
−
4
sin
B
=
−
7
tan
B
−
4
sin
C
=
−
7
tan
C
+
4
sin
A
=
−
7
{\displaystyle {\begin{array}{ccccl}\tan A\!&\!-\!&\!4\sin B\!&\!=\!&\!-{\sqrt {7}}\\[2pt]\tan B\!&\!-\!&\!4\sin C\!&\!=\!&\!-{\sqrt {7}}\\[2pt]\tan C\!&\!+\!&\!4\sin A\!&\!=\!&\!-{\sqrt {7}}\end{array}}}
[7] [8]
cot
2
A
=
1
−
2
tan
C
7
cot
2
B
=
1
−
2
tan
A
7
cot
2
C
=
1
−
2
tan
B
7
{\displaystyle {\begin{aligned}\cot ^{2}\!A&=1-{\frac {2\tan C}{\sqrt {7}}}\\[2pt]\cot ^{2}\!B&=1-{\frac {2\tan A}{\sqrt {7}}}\\[2pt]\cot ^{2}\!C&=1-{\frac {2\tan B}{\sqrt {7}}}\end{aligned}}}
[4]
cos
A
=
−
1
2
+
4
7
×
sin
3
C
sec
A
=
2
+
4
×
cos
C
sec
A
=
6
−
8
×
sin
2
B
sec
A
=
4
−
16
7
×
sin
3
B
cot
A
=
7
+
8
7
×
sin
2
B
cot
A
=
3
7
+
4
7
×
cos
B
sin
2
A
=
1
2
+
1
2
×
cos
B
cos
2
A
=
3
4
+
2
7
×
sin
3
A
cot
2
A
=
3
+
8
7
×
sin
A
sin
3
A
=
−
7
8
+
7
4
×
cos
B
csc
3
A
=
−
6
7
+
2
7
×
tan
2
C
{\displaystyle {\begin{array}{rcccccl}\cos A\!&\!=\!&\!{\frac {-1}{2}}\!&\!+\!&\!{\frac {4}{\sqrt {7}}}\!&\!\times \!&\!\sin ^{3}\!C\\[2pt]\sec A\!&\!=\!&\!2\!&\!+\!&\!4\!&\!\times \!&\!\cos C\\[4pt]\sec A\!&\!=\!&\!6\!&\!-\!&\!8\!&\!\times \!&\!\sin ^{2}\!B\\[4pt]\sec A\!&\!=\!&\!4\!&\!-\!&\!{\frac {16}{\sqrt {7}}}\!&\!\times \!&\!\sin ^{3}\!B\\[2pt]\cot A\!&\!=\!&\!{\sqrt {7}}\!&\!+\!&\!{\frac {8}{\sqrt {7}}}\!&\!\times \!&\!\sin ^{2}\!B\\[2pt]\cot A\!&\!=\!&\!{\frac {3}{\sqrt {7}}}\!&\!+\!&\!{\frac {4}{\sqrt {7}}}\!&\!\times \!&\!\cos B\\[2pt]\sin ^{2}\!A\!&\!=\!&\!{\frac {1}{2}}\!&\!+\!&\!{\frac {1}{2}}\!&\!\times \!&\!\cos B\\[2pt]\cos ^{2}\!A\!&\!=\!&\!{\frac {3}{4}}\!&\!+\!&\!{\frac {2}{\sqrt {7}}}\!&\!\times \!&\!\sin ^{3}\!A\\[2pt]\cot ^{2}\!A\!&\!=\!&\!3\!&\!+\!&\!{\frac {8}{\sqrt {7}}}\!&\!\times \!&\!\sin A\\[2pt]\sin ^{3}\!A\!&\!=\!&\!{\frac {-{\sqrt {7}}}{8}}\!&\!+\!&\!{\frac {\sqrt {7}}{4}}\!&\!\times \!&\!\cos B\\[2pt]\csc ^{3}\!A\!&\!=\!&\!{\frac {-6}{\sqrt {7}}}\!&\!+\!&\!{\frac {2}{\sqrt {7}}}\!&\!\times \!&\!\tan ^{2}\!C\end{array}}}
[4]
sin
A
sin
B
−
sin
B
sin
C
+
sin
C
sin
A
=
0
{\displaystyle \sin A\sin B-\sin B\sin C+\sin C\sin A=0}
sin
3
B
sin
C
−
sin
3
C
sin
A
−
sin
3
A
sin
B
=
0
sin
B
sin
3
C
−
sin
C
sin
3
A
−
sin
A
sin
3
B
=
7
2
4
sin
4
B
sin
C
−
sin
4
C
sin
A
+
sin
4
A
sin
B
=
0
sin
B
sin
4
C
+
sin
C
sin
4
A
−
sin
A
sin
4
B
=
7
7
2
5
{\displaystyle {\begin{aligned}\sin ^{3}\!B\sin C-\sin ^{3}\!C\sin A-\sin ^{3}\!A\sin B&=0\\[3pt]\sin B\sin ^{3}\!C-\sin C\sin ^{3}\!A-\sin A\sin ^{3}\!B&={\frac {7}{2^{4}\!}}\\[2pt]\sin ^{4}\!B\sin C-\sin ^{4}\!C\sin A+\sin ^{4}\!A\sin B&=0\\[2pt]\sin B\sin ^{4}\!C+\sin C\sin ^{4}\!A-\sin A\sin ^{4}\!B&={\frac {7{\sqrt {7}}}{2^{5}}}\end{aligned}}}
sin
11
B
sin
3
C
−
sin
11
C
sin
3
A
−
sin
11
A
sin
3
B
=
0
sin
3
B
sin
11
C
−
sin
3
C
sin
11
A
−
sin
3
A
sin
11
B
=
7
3
⋅
17
2
14
{\displaystyle {\begin{aligned}\sin ^{11}\!B\sin ^{3}\!C-\sin ^{11}\!C\sin ^{3}\!A-\sin ^{11}\!A\sin ^{3}\!B&=0\\[2pt]\sin ^{3}\!B\sin ^{11}\!C-\sin ^{3}\!C\sin ^{11}\!A-\sin ^{3}\!A\sin ^{11}\!B&={\frac {7^{3}\cdot 17}{2^{14}}}\end{aligned}}}
[9] Cubic polynomials [ edit ] The cubic equation
64
y
3
−
112
y
2
+
56
y
−
7
=
0
{\displaystyle 64y^{3}-112y^{2}+56y-7=0}
[2] : p. 14
sin
2
A
,
sin
2
B
,
sin
2
C
.
{\displaystyle \sin ^{2}\!A,\ \sin ^{2}\!B,\ \sin ^{2}\!C.}
The positive solution of the cubic equation
x
3
+
x
2
−
2
x
−
1
=
0
{\displaystyle x^{3}+x^{2}-2x-1=0}
2
cos
B
.
{\displaystyle 2\cos B.}
[10] : p. 186–187
The roots of the cubic equation
x
3
−
7
2
x
2
+
7
8
=
0
{\displaystyle x^{3}-{\tfrac {\sqrt {7}}{2}}x^{2}+{\tfrac {\sqrt {7}}{8}}=0}
[4]
sin
2
A
,
sin
2
B
,
sin
2
C
.
{\displaystyle \sin 2A,\ \sin 2B,\ \sin 2C.}
The roots of the cubic equation
x
3
−
7
2
x
2
+
7
8
=
0
{\displaystyle x^{3}-{\tfrac {\sqrt {7}}{2}}x^{2}+{\tfrac {\sqrt {7}}{8}}=0}
−
sin
A
,
sin
B
,
sin
C
.
{\displaystyle -\sin A,\ \sin B,\ \sin C.}
The roots of the cubic equation
x
3
+
1
2
x
2
−
1
2
x
−
1
8
=
0
{\displaystyle x^{3}+{\tfrac {1}{2}}x^{2}-{\tfrac {1}{2}}x-{\tfrac {1}{8}}=0}
−
cos
A
,
cos
B
,
cos
C
.
{\displaystyle -\cos A,\ \cos B,\ \cos C.}
The roots of the cubic equation
x
3
+
7
x
2
−
7
x
+
7
=
0
{\displaystyle x^{3}+{\sqrt {7}}x^{2}-7x+{\sqrt {7}}=0}
tan
A
,
tan
B
,
tan
C
.
{\displaystyle \tan A,\ \tan B,\ \tan C.}
The roots of the cubic equation
x
3
−
21
x
2
+
35
x
−
7
=
0
{\displaystyle x^{3}-21x^{2}+35x-7=0}
tan
2
A
,
tan
2
B
,
tan
2
C
.
{\displaystyle \tan ^{2}\!A,\ \tan ^{2}\!B,\ \tan ^{2}\!C.}
Sequences [ edit ] For an integer n , let
S
(
n
)
=
(
−
sin
A
)
n
+
sin
n
B
+
sin
n
C
C
(
n
)
=
(
−
cos
A
)
n
+
cos
n
B
+
cos
n
C
T
(
n
)
=
tan
n
A
+
tan
n
B
+
tan
n
C
{\displaystyle {\begin{aligned}S(n)&=(-\sin A)^{n}+\sin ^{n}\!B+\sin ^{n}\!C\\[4pt]C(n)&=(-\cos A)^{n}+\cos ^{n}\!B+\cos ^{n}\!C\\[4pt]T(n)&=\tan ^{n}\!A+\tan ^{n}\!B+\tan ^{n}\!C\end{aligned}}}
Value of n :
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
S
(
n
)
{\displaystyle S(n)}
3
{\displaystyle \ 3\ }
7
2
{\displaystyle {\tfrac {\sqrt {7}}{2}}}
7
2
2
{\displaystyle {\tfrac {7}{2^{2}}}}
7
2
{\displaystyle {\tfrac {\sqrt {7}}{2}}}
7
⋅
3
2
4
{\displaystyle {\tfrac {7\cdot 3}{2^{4}}}}
7
7
2
4
{\displaystyle {\tfrac {7{\sqrt {7}}}{2^{4}}}}
7
⋅
5
2
5
{\displaystyle {\tfrac {7\cdot 5}{2^{5}}}}
7
2
7
2
7
{\displaystyle {\tfrac {7^{2}{\sqrt {7}}}{2^{7}}}}
7
2
⋅
5
2
8
{\displaystyle {\tfrac {7^{2}\cdot 5}{2^{8}}}}
7
⋅
25
7
2
9
{\displaystyle {\tfrac {7\cdot 25{\sqrt {7}}}{2^{9}}}}
7
2
⋅
9
2
9
{\displaystyle {\tfrac {7^{2}\cdot 9}{2^{9}}}}
7
2
⋅
13
7
2
11
{\displaystyle {\tfrac {7^{2}\cdot 13{\sqrt {7}}}{2^{11}}}}
7
2
⋅
33
2
11
{\displaystyle {\tfrac {7^{2}\cdot 33}{2^{11}}}}
7
2
⋅
3
7
2
9
{\displaystyle {\tfrac {7^{2}\cdot 3{\sqrt {7}}}{2^{9}}}}
7
4
⋅
5
2
14
{\displaystyle {\tfrac {7^{4}\cdot 5}{2^{14}}}}
7
2
⋅
179
7
2
15
{\displaystyle {\tfrac {7^{2}\cdot 179{\sqrt {7}}}{2^{15}}}}
7
3
⋅
131
2
16
{\displaystyle {\tfrac {7^{3}\cdot 131}{2^{16}}}}
7
3
⋅
3
7
2
12
{\displaystyle {\tfrac {7^{3}\cdot 3{\sqrt {7}}}{2^{12}}}}
7
3
⋅
493
2
18
{\displaystyle {\tfrac {7^{3}\cdot 493}{2^{18}}}}
7
3
⋅
181
7
2
18
{\displaystyle {\tfrac {7^{3}\cdot 181{\sqrt {7}}}{2^{18}}}}
7
5
⋅
19
2
19
{\displaystyle {\tfrac {7^{5}\cdot 19}{2^{19}}}}
S
(
−
n
)
{\displaystyle S(-n)}
3
{\displaystyle 3}
0
{\displaystyle 0}
2
3
{\displaystyle 2^{3}}
−
2
3
⋅
3
7
7
{\displaystyle -{\tfrac {2^{3}\cdot 3{\sqrt {7}}}{7}}}
2
5
{\displaystyle 2^{5}}
−
2
5
⋅
5
7
7
{\displaystyle -{\tfrac {2^{5}\cdot 5{\sqrt {7}}}{7}}}
2
6
⋅
17
7
{\displaystyle {\tfrac {2^{6}\cdot 17}{7}}}
−
2
7
7
{\displaystyle -2^{7}{\sqrt {7}}}
2
9
⋅
11
7
{\displaystyle {\tfrac {2^{9}\cdot 11}{7}}}
−
2
10
⋅
33
7
7
2
{\displaystyle -{\tfrac {2^{10}\cdot 33{\sqrt {7}}}{7^{2}}}}
2
10
⋅
29
7
{\displaystyle {\tfrac {2^{10}\cdot 29}{7}}}
−
2
14
⋅
11
7
7
2
{\displaystyle -{\tfrac {2^{14}\cdot 11{\sqrt {7}}}{7^{2}}}}
2
12
⋅
269
7
2
{\displaystyle {\tfrac {2^{12}\cdot 269}{7^{2}}}}
−
2
13
⋅
117
7
7
2
{\displaystyle -{\tfrac {2^{13}\cdot 117{\sqrt {7}}}{7^{2}}}}
2
14
⋅
51
7
{\displaystyle {\tfrac {2^{14}\cdot 51}{7}}}
−
2
21
⋅
17
7
7
3
{\displaystyle -{\tfrac {2^{21}\cdot 17{\sqrt {7}}}{7^{3}}}}
2
17
⋅
237
7
2
{\displaystyle {\tfrac {2^{17}\cdot 237}{7^{2}}}}
−
2
17
⋅
1445
7
7
3
{\displaystyle -{\tfrac {2^{17}\cdot 1445{\sqrt {7}}}{7^{3}}}}
2
19
⋅
2203
7
3
{\displaystyle {\tfrac {2^{19}\cdot 2203}{7^{3}}}}
−
2
19
⋅
1919
7
7
3
{\displaystyle -{\tfrac {2^{19}\cdot 1919{\sqrt {7}}}{7^{3}}}}
2
20
⋅
5851
7
3
{\displaystyle {\tfrac {2^{20}\cdot 5851}{7^{3}}}}
C
(
n
)
{\displaystyle C(n)}
3
{\displaystyle 3}
−
1
2
{\displaystyle -{\tfrac {1}{2}}}
5
4
{\displaystyle {\tfrac {5}{4}}}
−
1
2
{\displaystyle -{\tfrac {1}{2}}}
13
16
{\displaystyle {\tfrac {13}{16}}}
−
1
2
{\displaystyle -{\tfrac {1}{2}}}
19
32
{\displaystyle {\tfrac {19}{32}}}
−
57
128
{\displaystyle -{\tfrac {57}{128}}}
117
256
{\displaystyle {\tfrac {117}{256}}}
−
193
512
{\displaystyle -{\tfrac {193}{512}}}
185
512
{\displaystyle {\tfrac {185}{512}}}
C
(
−
n
)
{\displaystyle C(-n)}
3
{\displaystyle 3}
−
4
{\displaystyle -4}
24
{\displaystyle 24}
−
88
{\displaystyle -88}
416
{\displaystyle 416}
−
1824
{\displaystyle -1824}
8256
{\displaystyle 8256}
−
36992
{\displaystyle -36992}
166400
{\displaystyle 166400}
−
747520
{\displaystyle -747520}
3359744
{\displaystyle 3359744}
T
(
n
)
{\displaystyle T(n)}
3
{\displaystyle 3}
−
7
{\displaystyle -{\sqrt {7}}}
7
⋅
3
{\displaystyle 7\cdot 3}
−
31
7
{\displaystyle -31{\sqrt {7}}}
7
⋅
53
{\displaystyle 7\cdot 53}
−
7
⋅
87
7
{\displaystyle -7\cdot 87{\sqrt {7}}}
7
⋅
1011
{\displaystyle 7\cdot 1011}
−
7
2
⋅
239
7
{\displaystyle -7^{2}\cdot 239{\sqrt {7}}}
7
2
⋅
2771
{\displaystyle 7^{2}\cdot 2771}
−
7
⋅
32119
7
{\displaystyle -7\cdot 32119{\sqrt {7}}}
7
2
⋅
53189
{\displaystyle 7^{2}\cdot 53189}
T
(
−
n
)
{\displaystyle T(-n)}
3
{\displaystyle 3}
7
{\displaystyle {\sqrt {7}}}
5
{\displaystyle 5}
25
7
7
{\displaystyle {\tfrac {25{\sqrt {7}}}{7}}}
19
{\displaystyle 19}
103
7
7
{\displaystyle {\tfrac {103{\sqrt {7}}}{7}}}
563
7
{\displaystyle {\tfrac {563}{7}}}
7
⋅
9
7
{\displaystyle 7\cdot 9{\sqrt {7}}}
2421
7
{\displaystyle {\tfrac {2421}{7}}}
13297
7
7
2
{\displaystyle {\tfrac {13297{\sqrt {7}}}{7^{2}}}}
10435
7
{\displaystyle {\tfrac {10435}{7}}}
Ramanujan identities [ edit ] We also have Ramanujan type identities,[7] [11]
2
sin
2
A
3
+
2
sin
2
B
3
+
2
sin
2
C
3
=
−
7
18
×
−
7
3
+
6
+
3
(
5
−
3
7
3
3
+
4
−
3
7
3
3
)
3
2
sin
2
A
3
+
2
sin
2
B
3
+
2
sin
2
C
3
=
−
7
18
×
−
7
3
+
6
+
3
(
5
−
3
7
3
3
+
4
−
3
7
3
3
)
3
4
sin
2
2
A
3
+
4
sin
2
2
B
3
+
4
sin
2
2
C
3
=
49
18
×
49
3
+
6
+
3
(
12
+
3
(
49
3
+
2
7
3
)
3
+
11
+
3
(
49
3
+
2
7
3
)
3
)
3
2
cos
2
A
3
+
2
cos
2
B
3
+
2
cos
2
C
3
=
5
−
3
7
3
3
4
cos
2
2
A
3
+
4
cos
2
2
B
3
+
4
cos
2
2
C
3
=
11
+
3
(
2
7
3
+
49
3
)
3
tan
2
A
3
+
tan
2
B
3
+
tan
2
C
3
=
−
7
18
×
7
3
+
6
+
3
(
5
+
3
(
7
3
−
49
3
)
3
+
−
3
+
3
(
7
3
−
49
3
)
3
)
3
tan
2
2
A
3
+
tan
2
2
B
3
+
tan
2
2
C
3
=
49
18
×
3
49
3
+
6
+
3
(
89
+
3
(
3
49
3
+
5
7
3
)
3
+
25
+
3
(
3
49
3
+
5
7
3
)
3
)
3
{\displaystyle {\begin{array}{ccccccl}{\sqrt[{3}]{2\sin 2A}}\!&\!+\!&\!{\sqrt[{3}]{2\sin 2B}}\!&\!+\!&\!{\sqrt[{3}]{2\sin 2C}}\!&\!=\!&\!-{\sqrt[{18}]{7}}\times {\sqrt[{3}]{-{\sqrt[{3}]{7}}+6+3\left({\sqrt[{3}]{5-3{\sqrt[{3}]{7}}}}+{\sqrt[{3}]{4-3{\sqrt[{3}]{7}}}}\right)}}\\[2pt]{\sqrt[{3}]{2\sin 2A}}\!&\!+\!&\!{\sqrt[{3}]{2\sin 2B}}\!&\!+\!&\!{\sqrt[{3}]{2\sin 2C}}\!&\!=\!&\!-{\sqrt[{18}]{7}}\times {\sqrt[{3}]{-{\sqrt[{3}]{7}}+6+3\left({\sqrt[{3}]{5-3{\sqrt[{3}]{7}}}}+{\sqrt[{3}]{4-3{\sqrt[{3}]{7}}}}\right)}}\\[2pt]{\sqrt[{3}]{4\sin ^{2}2A}}\!&\!+\!&\!{\sqrt[{3}]{4\sin ^{2}2B}}\!&\!+\!&\!{\sqrt[{3}]{4\sin ^{2}2C}}\!&\!=\!&\!{\sqrt[{18}]{49}}\times {\sqrt[{3}]{{\sqrt[{3}]{49}}+6+3\left({\sqrt[{3}]{12+3({\sqrt[{3}]{49}}+2{\sqrt[{3}]{7}})}}+{\sqrt[{3}]{11+3({\sqrt[{3}]{49}}+2{\sqrt[{3}]{7}})}}\right)}}\\[6pt]{\sqrt[{3}]{2\cos 2A}}\!&\!+\!&\!{\sqrt[{3}]{2\cos 2B}}\!&\!+\!&\!{\sqrt[{3}]{2\cos 2C}}\!&\!=\!&\!{\sqrt[{3}]{5-3{\sqrt[{3}]{7}}}}\\[8pt]{\sqrt[{3}]{4\cos ^{2}2A}}\!&\!+\!&\!{\sqrt[{3}]{4\cos ^{2}2B}}\!&\!+\!&\!{\sqrt[{3}]{4\cos ^{2}2C}}\!&\!=\!&\!{\sqrt[{3}]{11+3(2{\sqrt[{3}]{7}}+{\sqrt[{3}]{49}})}}\\[6pt]{\sqrt[{3}]{\tan 2A}}\!&\!+\!&\!{\sqrt[{3}]{\tan 2B}}\!&\!+\!&\!{\sqrt[{3}]{\tan 2C}}\!&\!=\!&\!-{\sqrt[{18}]{7}}\times {\sqrt[{3}]{{\sqrt[{3}]{7}}+6+3\left({\sqrt[{3}]{5+3({\sqrt[{3}]{7}}-{\sqrt[{3}]{49}})}}+{\sqrt[{3}]{-3+3({\sqrt[{3}]{7}}-{\sqrt[{3}]{49}})}}\right)}}\\[2pt]{\sqrt[{3}]{\tan ^{2}2A}}\!&\!+\!&\!{\sqrt[{3}]{\tan ^{2}2B}}\!&\!+\!&\!{\sqrt[{3}]{\tan ^{2}2C}}\!&\!=\!&\!{\sqrt[{18}]{49}}\times {\sqrt[{3}]{3{\sqrt[{3}]{49}}+6+3\left({\sqrt[{3}]{89+3(3{\sqrt[{3}]{49}}+5{\sqrt[{3}]{7}})}}+{\sqrt[{3}]{25+3(3{\sqrt[{3}]{49}}+5{\sqrt[{3}]{7}})}}\right)}}\end{array}}}
1
2
sin
2
A
3
+
1
2
sin
2
B
3
+
1
2
sin
2
C
3
=
−
1
7
18
×
6
+
3
(
5
−
3
7
3
3
+
4
−
3
7
3
3
)
3
1
4
sin
2
2
A
3
+
1
4
sin
2
2
B
3
+
1
4
sin
2
2
C
3
=
1
49
18
×
2
7
3
+
6
+
3
(
12
+
3
(
49
3
+
2
7
3
)
3
+
11
+
3
(
49
3
+
2
7
3
)
3
)
3
1
2
cos
2
A
3
+
1
2
cos
2
B
3
+
1
2
cos
2
C
3
=
4
−
3
7
3
3
1
4
cos
2
2
A
3
+
1
4
cos
2
2
B
3
+
1
4
cos
2
2
C
3
=
12
+
3
(
2
7
3
+
49
3
)
3
1
tan
2
A
3
+
1
tan
2
B
3
+
1
tan
2
C
3
=
−
1
7
18
×
−
49
3
+
6
+
3
(
5
+
3
(
7
3
−
49
3
)
3
+
−
3
+
3
(
7
3
−
49
3
)
3
)
3
1
tan
2
2
A
3
+
1
tan
2
2
B
3
+
1
tan
2
2
C
3
=
1
49
18
×
5
7
3
+
6
+
3
(
89
+
3
(
3
49
3
+
5
7
3
)
3
+
25
+
3
(
3
49
3
+
5
7
3
)
3
)
3
{\displaystyle {\begin{array}{ccccccl}{\frac {1}{\sqrt[{3}]{2\sin 2A}}}\!&\!+\!&\!{\frac {1}{\sqrt[{3}]{2\sin 2B}}}\!&\!+\!&\!{\frac {1}{\sqrt[{3}]{2\sin 2C}}}\!&\!=\!&\!-{\frac {1}{\sqrt[{18}]{7}}}\times {\sqrt[{3}]{6+3\left({\sqrt[{3}]{5-3{\sqrt[{3}]{7}}}}+{\sqrt[{3}]{4-3{\sqrt[{3}]{7}}}}\right)}}\\[2pt]{\frac {1}{\sqrt[{3}]{4\sin ^{2}2A}}}\!&\!+\!&\!{\frac {1}{\sqrt[{3}]{4\sin ^{2}2B}}}\!&\!+\!&\!{\frac {1}{\sqrt[{3}]{4\sin ^{2}2C}}}\!&\!=\!&\!{\frac {1}{\sqrt[{18}]{49}}}\times {\sqrt[{3}]{2{\sqrt[{3}]{7}}+6+3\left({\sqrt[{3}]{12+3({\sqrt[{3}]{49}}+2{\sqrt[{3}]{7}})}}+{\sqrt[{3}]{11+3({\sqrt[{3}]{49}}+2{\sqrt[{3}]{7}})}}\right)}}\\[2pt]{\frac {1}{\sqrt[{3}]{2\cos 2A}}}\!&\!+\!&\!{\frac {1}{\sqrt[{3}]{2\cos 2B}}}\!&\!+\!&\!{\frac {1}{\sqrt[{3}]{2\cos 2C}}}\!&\!=\!&\!{\sqrt[{3}]{4-3{\sqrt[{3}]{7}}}}\\[6pt]{\frac {1}{\sqrt[{3}]{4\cos ^{2}2A}}}\!&\!+\!&\!{\frac {1}{\sqrt[{3}]{4\cos ^{2}2B}}}\!&\!+\!&\!{\frac {1}{\sqrt[{3}]{4\cos ^{2}2C}}}\!&\!=\!&\!{\sqrt[{3}]{12+3(2{\sqrt[{3}]{7}}+{\sqrt[{3}]{49}})}}\\[2pt]{\frac {1}{\sqrt[{3}]{\tan 2A}}}\!&\!+\!&\!{\frac {1}{\sqrt[{3}]{\tan 2B}}}\!&\!+\!&\!{\frac {1}{\sqrt[{3}]{\tan 2C}}}\!&\!=\!&\!-{\frac {1}{\sqrt[{18}]{7}}}\times {\sqrt[{3}]{-{\sqrt[{3}]{49}}+6+3\left({\sqrt[{3}]{5+3({\sqrt[{3}]{7}}-{\sqrt[{3}]{49}})}}+{\sqrt[{3}]{-3+3({\sqrt[{3}]{7}}-{\sqrt[{3}]{49}})}}\right)}}\\[2pt]{\frac {1}{\sqrt[{3}]{\tan ^{2}2A}}}\!&\!+\!&\!{\frac {1}{\sqrt[{3}]{\tan ^{2}2B}}}\!&\!+\!&\!{\frac {1}{\sqrt[{3}]{\tan ^{2}2C}}}\!&\!=\!&\!{\frac {1}{\sqrt[{18}]{49}}}\times {\sqrt[{3}]{5{\sqrt[{3}]{7}}+6+3\left({\sqrt[{3}]{89+3(3{\sqrt[{3}]{49}}+5{\sqrt[{3}]{7}})}}+{\sqrt[{3}]{25+3(3{\sqrt[{3}]{49}}+5{\sqrt[{3}]{7}})}}\right)}}\end{array}}}
cos
2
A
cos
2
B
3
+
cos
2
B
cos
2
C
3
+
cos
2
C
cos
2
A
3
=
−
7
3
cos
2
B
cos
2
A
3
+
cos
2
C
cos
2
B
3
+
cos
2
A
cos
2
C
3
=
0
cos
4
2
B
cos
2
A
3
+
cos
4
2
C
cos
2
B
3
+
cos
4
2
A
cos
2
C
3
=
−
49
3
2
cos
5
2
A
cos
2
2
B
3
+
cos
5
2
B
cos
2
2
C
3
+
cos
5
2
C
cos
2
2
A
3
=
0
cos
5
2
B
cos
2
2
A
3
+
cos
5
2
C
cos
2
2
B
3
+
cos
5
2
A
cos
2
2
C
3
=
−
3
×
7
3
2
cos
14
2
A
cos
5
2
B
3
+
cos
14
2
B
cos
5
2
C
3
+
cos
14
2
C
cos
5
2
A
3
=
0
cos
14
2
B
cos
5
2
A
3
+
cos
14
2
C
cos
5
2
B
3
+
cos
14
2
A
cos
5
2
C
3
=
−
61
×
7
3
8
.
{\displaystyle {\begin{array}{ccccccl}{\sqrt[{3}]{\frac {\cos 2A}{\cos 2B}}}\!&\!+\!&\!{\sqrt[{3}]{\frac {\cos 2B}{\cos 2C}}}\!&\!+\!&\!{\sqrt[{3}]{\frac {\cos 2C}{\cos 2A}}}\!&\!=\!&\!-{\sqrt[{3}]{7}}\\[2pt]{\sqrt[{3}]{\frac {\cos 2B}{\cos 2A}}}\!&\!+\!&\!{\sqrt[{3}]{\frac {\cos 2C}{\cos 2B}}}\!&\!+\!&\!{\sqrt[{3}]{\frac {\cos 2A}{\cos 2C}}}\!&\!=\!&\!0\\[2pt]{\sqrt[{3}]{\frac {\cos ^{4}2B}{\cos 2A}}}\!&\!+\!&\!{\sqrt[{3}]{\frac {\cos ^{4}2C}{\cos 2B}}}\!&\!+\!&\!{\sqrt[{3}]{\frac {\cos ^{4}2A}{\cos 2C}}}\!&\!=\!&\!-{\frac {\sqrt[{3}]{49}}{2}}\\[2pt]{\sqrt[{3}]{\frac {\cos ^{5}2A}{\cos ^{2}2B}}}\!&\!+\!&\!{\sqrt[{3}]{\frac {\cos ^{5}2B}{\cos ^{2}2C}}}\!&\!+\!&\!{\sqrt[{3}]{\frac {\cos ^{5}2C}{\cos ^{2}2A}}}\!&\!=\!&\!0\\[2pt]{\sqrt[{3}]{\frac {\cos ^{5}2B}{\cos ^{2}2A}}}\!&\!+\!&\!{\sqrt[{3}]{\frac {\cos ^{5}2C}{\cos ^{2}2B}}}\!&\!+\!&\!{\sqrt[{3}]{\frac {\cos ^{5}2A}{\cos ^{2}2C}}}\!&\!=\!&\!-3\times {\frac {\sqrt[{3}]{7}}{2}}\\[2pt]{\sqrt[{3}]{\frac {\cos ^{14}2A}{\cos ^{5}2B}}}\!&\!+\!&\!{\sqrt[{3}]{\frac {\cos ^{14}2B}{\cos ^{5}2C}}}\!&\!+\!&\!{\sqrt[{3}]{\frac {\cos ^{14}2C}{\cos ^{5}2A}}}\!&\!=\!&\!0\\[2pt]{\sqrt[{3}]{\frac {\cos ^{14}2B}{\cos ^{5}2A}}}\!&\!+\!&\!{\sqrt[{3}]{\frac {\cos ^{14}2C}{\cos ^{5}2B}}}\!&\!+\!&\!{\sqrt[{3}]{\frac {\cos ^{14}2A}{\cos ^{5}2C}}}\!&\!=\!&\!-61\times {\frac {\sqrt[{3}]{7}}{8}}.\end{array}}}
[9]
References [ edit ]
^ a b Paul Yiu, "Heptagonal Triangles and Their Companions", Forum Geometricorum http://forumgeom.fau.edu/FG2009volume9/FG200912.pdf
^ a b c d e f g h i j k l m n o p q Leon Bankoff and Jack Garfunkel, "The heptagonal triangle", Mathematics Magazine
^ a b Abdilkadir Altintas, "Some Collinearities in the Heptagonal Triangle", Forum Geometricorum http://forumgeom.fau.edu/FG2016volume16/FG201630.pdf
^ a b c d e f g h i Wang, Kai. “Heptagonal Triangle and Trigonometric Identities”, Forum Geometricorum 19, 2019, 29–38.
^ Wang, Kai.
https://www.researchgate.net/publication/335392159_On_cubic_equations_with_zero_sums_of_cubic_roots_of_roots
^ a b c Weisstein, Eric W. "Heptagonal Triangle." From MathWorld--A Wolfram Web Resource. http://mathworld.wolfram.com/HeptagonalTriangle.html
^ a b c d e f Wang, Kai. https://www.researchgate.net/publication/327825153_Trigonometric_Properties_For_Heptagonal_Triangle
^ Victor Hugo Moll , An elementary trigonometric equation, https://arxiv.org/abs/0709.3755 , 2007^ a b Wang, Kai.
https://www.researchgate.net/publication/336813631_Topics_of_Ramanujan_type_identities_for_PI7
^ Gleason, Andrew Mattei (March 1988). "Angle trisection, the heptagon, and the triskaidecagon" (PDF) . The American Mathematical Monthly . 95 (3): 185–194. doi :10.2307/2323624 . Archived from the original (PDF) on 2015-12-19. ^ Roman Witula and Damian Slota, New Ramanujan-Type Formulas and Quasi-Fibonacci Numbers of Order 7, Journal of Integer Sequences, Vol. 10 (2007).





![{\displaystyle {\begin{aligned}a^{2}&=c(c-b),\\[5pt]b^{2}&=a(c+a),\\[5pt]c^{2}&=b(a+b),\\[5pt]{\frac {1}{a}}&={\frac {1}{b}}+{\frac {1}{c}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/63107bd555aab31d4dbd45b3bea63fcb044aeb43)













































![{\displaystyle {\begin{aligned}A&={\frac {\pi }{7}}\\[6pt]\cos A&={\frac {b}{2a}}\end{aligned}}\quad {\begin{aligned}B&={\frac {2\pi }{7}}\\[6pt]\cos B&={\frac {c}{2b}}\end{aligned}}\quad {\begin{aligned}C&={\frac {4\pi }{7}}\\[6pt]\cos C&=-{\frac {a}{2c}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/95dd39d97a0beffeae6cda91521c6eca64ade86a)
![{\displaystyle {\begin{array}{rcccccl}\sin A\!&\!\times \!&\!\sin B\!&\!\times \!&\!\sin C\!&\!=\!&\!{\frac {\sqrt {7}}{8}}\\[2pt]\sin A\!&\!-\!&\!\sin B\!&\!-\!&\!\sin C\!&\!=\!&\!-{\frac {\sqrt {7}}{2}}\\[2pt]\cos A\!&\!\times \!&\!\cos B\!&\!\times \!&\!\cos C\!&\!=\!&\!-{\frac {1}{8}}\\[2pt]\tan A\!&\!\times \!&\!\tan B\!&\!\times \!&\!\tan C\!&\!=\!&\!-{\sqrt {7}}\\[2pt]\tan A\!&\!+\!&\!\tan B\!&\!+\!&\!\tan C\!&\!=\!&\!-{\sqrt {7}}\\[2pt]\cot A\!&\!+\!&\!\cot B\!&\!+\!&\!\cot C\!&\!=\!&\!{\sqrt {7}}\\[8pt]\sin ^{2}\!A\!&\!\times \!&\!\sin ^{2}\!B\!&\!\times \!&\!\sin ^{2}\!C\!&\!=\!&\!{\frac {7}{64}}\\[2pt]\sin ^{2}\!A\!&\!+\!&\!\sin ^{2}\!B\!&\!+\!&\!\sin ^{2}\!C\!&\!=\!&\!{\frac {7}{4}}\\[2pt]\cos ^{2}\!A\!&\!+\!&\!\cos ^{2}\!B\!&\!+\!&\!\cos ^{2}\!C\!&\!=\!&\!{\frac {5}{4}}\\[2pt]\tan ^{2}\!A\!&\!+\!&\!\tan ^{2}\!B\!&\!+\!&\!\tan ^{2}\!C\!&\!=\!&\!21\\[2pt]\sec ^{2}\!A\!&\!+\!&\!\sec ^{2}\!B\!&\!+\!&\!\sec ^{2}\!C\!&\!=\!&\!24\\[2pt]\csc ^{2}\!A\!&\!+\!&\!\csc ^{2}\!B\!&\!+\!&\!\csc ^{2}\!C\!&\!=\!&\!8\\[2pt]\cot ^{2}\!A\!&\!+\!&\!\cot ^{2}\!B\!&\!+\!&\!\cot ^{2}\!C\!&\!=\!&\!5\\[8pt]\sin ^{4}\!A\!&\!+\!&\!\sin ^{4}\!B\!&\!+\!&\!\sin ^{4}\!C\!&\!=\!&\!{\frac {21}{16}}\\[2pt]\cos ^{4}\!A\!&\!+\!&\!\cos ^{4}\!B\!&\!+\!&\!\cos ^{4}\!C\!&\!=\!&\!{\frac {13}{16}}\\[2pt]\sec ^{4}\!A\!&\!+\!&\!\sec ^{4}\!B\!&\!+\!&\!\sec ^{4}\!C\!&\!=\!&\!416\\[2pt]\csc ^{4}\!A\!&\!+\!&\!\csc ^{4}\!B\!&\!+\!&\!\csc ^{4}\!C\!&\!=\!&\!32\\[8pt]\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/11372d01f064a3ac9ffba8d9f82ccf67392e62ed)
![{\displaystyle {\begin{array}{ccccl}\tan A\!&\!-\!&\!4\sin B\!&\!=\!&\!-{\sqrt {7}}\\[2pt]\tan B\!&\!-\!&\!4\sin C\!&\!=\!&\!-{\sqrt {7}}\\[2pt]\tan C\!&\!+\!&\!4\sin A\!&\!=\!&\!-{\sqrt {7}}\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e81c6d96fd69af254e9ce675fad313b333fd7904)
![{\displaystyle {\begin{aligned}\cot ^{2}\!A&=1-{\frac {2\tan C}{\sqrt {7}}}\\[2pt]\cot ^{2}\!B&=1-{\frac {2\tan A}{\sqrt {7}}}\\[2pt]\cot ^{2}\!C&=1-{\frac {2\tan B}{\sqrt {7}}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/50839aa6272436a1b2888172a7c95235431e7688)
![{\displaystyle {\begin{array}{rcccccl}\cos A\!&\!=\!&\!{\frac {-1}{2}}\!&\!+\!&\!{\frac {4}{\sqrt {7}}}\!&\!\times \!&\!\sin ^{3}\!C\\[2pt]\sec A\!&\!=\!&\!2\!&\!+\!&\!4\!&\!\times \!&\!\cos C\\[4pt]\sec A\!&\!=\!&\!6\!&\!-\!&\!8\!&\!\times \!&\!\sin ^{2}\!B\\[4pt]\sec A\!&\!=\!&\!4\!&\!-\!&\!{\frac {16}{\sqrt {7}}}\!&\!\times \!&\!\sin ^{3}\!B\\[2pt]\cot A\!&\!=\!&\!{\sqrt {7}}\!&\!+\!&\!{\frac {8}{\sqrt {7}}}\!&\!\times \!&\!\sin ^{2}\!B\\[2pt]\cot A\!&\!=\!&\!{\frac {3}{\sqrt {7}}}\!&\!+\!&\!{\frac {4}{\sqrt {7}}}\!&\!\times \!&\!\cos B\\[2pt]\sin ^{2}\!A\!&\!=\!&\!{\frac {1}{2}}\!&\!+\!&\!{\frac {1}{2}}\!&\!\times \!&\!\cos B\\[2pt]\cos ^{2}\!A\!&\!=\!&\!{\frac {3}{4}}\!&\!+\!&\!{\frac {2}{\sqrt {7}}}\!&\!\times \!&\!\sin ^{3}\!A\\[2pt]\cot ^{2}\!A\!&\!=\!&\!3\!&\!+\!&\!{\frac {8}{\sqrt {7}}}\!&\!\times \!&\!\sin A\\[2pt]\sin ^{3}\!A\!&\!=\!&\!{\frac {-{\sqrt {7}}}{8}}\!&\!+\!&\!{\frac {\sqrt {7}}{4}}\!&\!\times \!&\!\cos B\\[2pt]\csc ^{3}\!A\!&\!=\!&\!{\frac {-6}{\sqrt {7}}}\!&\!+\!&\!{\frac {2}{\sqrt {7}}}\!&\!\times \!&\!\tan ^{2}\!C\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b36fe1e7d4ad29454a0aa79868851380c420711c)

![{\displaystyle {\begin{aligned}\sin ^{3}\!B\sin C-\sin ^{3}\!C\sin A-\sin ^{3}\!A\sin B&=0\\[3pt]\sin B\sin ^{3}\!C-\sin C\sin ^{3}\!A-\sin A\sin ^{3}\!B&={\frac {7}{2^{4}\!}}\\[2pt]\sin ^{4}\!B\sin C-\sin ^{4}\!C\sin A+\sin ^{4}\!A\sin B&=0\\[2pt]\sin B\sin ^{4}\!C+\sin C\sin ^{4}\!A-\sin A\sin ^{4}\!B&={\frac {7{\sqrt {7}}}{2^{5}}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/313eecf9c55707e7d80590c5350d7c1c461b8b1d)
![{\displaystyle {\begin{aligned}\sin ^{11}\!B\sin ^{3}\!C-\sin ^{11}\!C\sin ^{3}\!A-\sin ^{11}\!A\sin ^{3}\!B&=0\\[2pt]\sin ^{3}\!B\sin ^{11}\!C-\sin ^{3}\!C\sin ^{11}\!A-\sin ^{3}\!A\sin ^{11}\!B&={\frac {7^{3}\cdot 17}{2^{14}}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/04ff05b82052d8332beefe762209d7d4e1f67d72)













![{\displaystyle {\begin{aligned}S(n)&=(-\sin A)^{n}+\sin ^{n}\!B+\sin ^{n}\!C\\[4pt]C(n)&=(-\cos A)^{n}+\cos ^{n}\!B+\cos ^{n}\!C\\[4pt]T(n)&=\tan ^{n}\!A+\tan ^{n}\!B+\tan ^{n}\!C\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/30746680912c548893246cbf950126c4bed81f68)





















































































![{\displaystyle {\begin{array}{ccccccl}{\sqrt[{3}]{2\sin 2A}}\!&\!+\!&\!{\sqrt[{3}]{2\sin 2B}}\!&\!+\!&\!{\sqrt[{3}]{2\sin 2C}}\!&\!=\!&\!-{\sqrt[{18}]{7}}\times {\sqrt[{3}]{-{\sqrt[{3}]{7}}+6+3\left({\sqrt[{3}]{5-3{\sqrt[{3}]{7}}}}+{\sqrt[{3}]{4-3{\sqrt[{3}]{7}}}}\right)}}\\[2pt]{\sqrt[{3}]{2\sin 2A}}\!&\!+\!&\!{\sqrt[{3}]{2\sin 2B}}\!&\!+\!&\!{\sqrt[{3}]{2\sin 2C}}\!&\!=\!&\!-{\sqrt[{18}]{7}}\times {\sqrt[{3}]{-{\sqrt[{3}]{7}}+6+3\left({\sqrt[{3}]{5-3{\sqrt[{3}]{7}}}}+{\sqrt[{3}]{4-3{\sqrt[{3}]{7}}}}\right)}}\\[2pt]{\sqrt[{3}]{4\sin ^{2}2A}}\!&\!+\!&\!{\sqrt[{3}]{4\sin ^{2}2B}}\!&\!+\!&\!{\sqrt[{3}]{4\sin ^{2}2C}}\!&\!=\!&\!{\sqrt[{18}]{49}}\times {\sqrt[{3}]{{\sqrt[{3}]{49}}+6+3\left({\sqrt[{3}]{12+3({\sqrt[{3}]{49}}+2{\sqrt[{3}]{7}})}}+{\sqrt[{3}]{11+3({\sqrt[{3}]{49}}+2{\sqrt[{3}]{7}})}}\right)}}\\[6pt]{\sqrt[{3}]{2\cos 2A}}\!&\!+\!&\!{\sqrt[{3}]{2\cos 2B}}\!&\!+\!&\!{\sqrt[{3}]{2\cos 2C}}\!&\!=\!&\!{\sqrt[{3}]{5-3{\sqrt[{3}]{7}}}}\\[8pt]{\sqrt[{3}]{4\cos ^{2}2A}}\!&\!+\!&\!{\sqrt[{3}]{4\cos ^{2}2B}}\!&\!+\!&\!{\sqrt[{3}]{4\cos ^{2}2C}}\!&\!=\!&\!{\sqrt[{3}]{11+3(2{\sqrt[{3}]{7}}+{\sqrt[{3}]{49}})}}\\[6pt]{\sqrt[{3}]{\tan 2A}}\!&\!+\!&\!{\sqrt[{3}]{\tan 2B}}\!&\!+\!&\!{\sqrt[{3}]{\tan 2C}}\!&\!=\!&\!-{\sqrt[{18}]{7}}\times {\sqrt[{3}]{{\sqrt[{3}]{7}}+6+3\left({\sqrt[{3}]{5+3({\sqrt[{3}]{7}}-{\sqrt[{3}]{49}})}}+{\sqrt[{3}]{-3+3({\sqrt[{3}]{7}}-{\sqrt[{3}]{49}})}}\right)}}\\[2pt]{\sqrt[{3}]{\tan ^{2}2A}}\!&\!+\!&\!{\sqrt[{3}]{\tan ^{2}2B}}\!&\!+\!&\!{\sqrt[{3}]{\tan ^{2}2C}}\!&\!=\!&\!{\sqrt[{18}]{49}}\times {\sqrt[{3}]{3{\sqrt[{3}]{49}}+6+3\left({\sqrt[{3}]{89+3(3{\sqrt[{3}]{49}}+5{\sqrt[{3}]{7}})}}+{\sqrt[{3}]{25+3(3{\sqrt[{3}]{49}}+5{\sqrt[{3}]{7}})}}\right)}}\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/810c85d0d2d0261c86d4ad110e55c03d4310c4f0)
![{\displaystyle {\begin{array}{ccccccl}{\frac {1}{\sqrt[{3}]{2\sin 2A}}}\!&\!+\!&\!{\frac {1}{\sqrt[{3}]{2\sin 2B}}}\!&\!+\!&\!{\frac {1}{\sqrt[{3}]{2\sin 2C}}}\!&\!=\!&\!-{\frac {1}{\sqrt[{18}]{7}}}\times {\sqrt[{3}]{6+3\left({\sqrt[{3}]{5-3{\sqrt[{3}]{7}}}}+{\sqrt[{3}]{4-3{\sqrt[{3}]{7}}}}\right)}}\\[2pt]{\frac {1}{\sqrt[{3}]{4\sin ^{2}2A}}}\!&\!+\!&\!{\frac {1}{\sqrt[{3}]{4\sin ^{2}2B}}}\!&\!+\!&\!{\frac {1}{\sqrt[{3}]{4\sin ^{2}2C}}}\!&\!=\!&\!{\frac {1}{\sqrt[{18}]{49}}}\times {\sqrt[{3}]{2{\sqrt[{3}]{7}}+6+3\left({\sqrt[{3}]{12+3({\sqrt[{3}]{49}}+2{\sqrt[{3}]{7}})}}+{\sqrt[{3}]{11+3({\sqrt[{3}]{49}}+2{\sqrt[{3}]{7}})}}\right)}}\\[2pt]{\frac {1}{\sqrt[{3}]{2\cos 2A}}}\!&\!+\!&\!{\frac {1}{\sqrt[{3}]{2\cos 2B}}}\!&\!+\!&\!{\frac {1}{\sqrt[{3}]{2\cos 2C}}}\!&\!=\!&\!{\sqrt[{3}]{4-3{\sqrt[{3}]{7}}}}\\[6pt]{\frac {1}{\sqrt[{3}]{4\cos ^{2}2A}}}\!&\!+\!&\!{\frac {1}{\sqrt[{3}]{4\cos ^{2}2B}}}\!&\!+\!&\!{\frac {1}{\sqrt[{3}]{4\cos ^{2}2C}}}\!&\!=\!&\!{\sqrt[{3}]{12+3(2{\sqrt[{3}]{7}}+{\sqrt[{3}]{49}})}}\\[2pt]{\frac {1}{\sqrt[{3}]{\tan 2A}}}\!&\!+\!&\!{\frac {1}{\sqrt[{3}]{\tan 2B}}}\!&\!+\!&\!{\frac {1}{\sqrt[{3}]{\tan 2C}}}\!&\!=\!&\!-{\frac {1}{\sqrt[{18}]{7}}}\times {\sqrt[{3}]{-{\sqrt[{3}]{49}}+6+3\left({\sqrt[{3}]{5+3({\sqrt[{3}]{7}}-{\sqrt[{3}]{49}})}}+{\sqrt[{3}]{-3+3({\sqrt[{3}]{7}}-{\sqrt[{3}]{49}})}}\right)}}\\[2pt]{\frac {1}{\sqrt[{3}]{\tan ^{2}2A}}}\!&\!+\!&\!{\frac {1}{\sqrt[{3}]{\tan ^{2}2B}}}\!&\!+\!&\!{\frac {1}{\sqrt[{3}]{\tan ^{2}2C}}}\!&\!=\!&\!{\frac {1}{\sqrt[{18}]{49}}}\times {\sqrt[{3}]{5{\sqrt[{3}]{7}}+6+3\left({\sqrt[{3}]{89+3(3{\sqrt[{3}]{49}}+5{\sqrt[{3}]{7}})}}+{\sqrt[{3}]{25+3(3{\sqrt[{3}]{49}}+5{\sqrt[{3}]{7}})}}\right)}}\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/092ce3486cbd674aa014182b557e6dbbd0a058b9)
![{\displaystyle {\begin{array}{ccccccl}{\sqrt[{3}]{\frac {\cos 2A}{\cos 2B}}}\!&\!+\!&\!{\sqrt[{3}]{\frac {\cos 2B}{\cos 2C}}}\!&\!+\!&\!{\sqrt[{3}]{\frac {\cos 2C}{\cos 2A}}}\!&\!=\!&\!-{\sqrt[{3}]{7}}\\[2pt]{\sqrt[{3}]{\frac {\cos 2B}{\cos 2A}}}\!&\!+\!&\!{\sqrt[{3}]{\frac {\cos 2C}{\cos 2B}}}\!&\!+\!&\!{\sqrt[{3}]{\frac {\cos 2A}{\cos 2C}}}\!&\!=\!&\!0\\[2pt]{\sqrt[{3}]{\frac {\cos ^{4}2B}{\cos 2A}}}\!&\!+\!&\!{\sqrt[{3}]{\frac {\cos ^{4}2C}{\cos 2B}}}\!&\!+\!&\!{\sqrt[{3}]{\frac {\cos ^{4}2A}{\cos 2C}}}\!&\!=\!&\!-{\frac {\sqrt[{3}]{49}}{2}}\\[2pt]{\sqrt[{3}]{\frac {\cos ^{5}2A}{\cos ^{2}2B}}}\!&\!+\!&\!{\sqrt[{3}]{\frac {\cos ^{5}2B}{\cos ^{2}2C}}}\!&\!+\!&\!{\sqrt[{3}]{\frac {\cos ^{5}2C}{\cos ^{2}2A}}}\!&\!=\!&\!0\\[2pt]{\sqrt[{3}]{\frac {\cos ^{5}2B}{\cos ^{2}2A}}}\!&\!+\!&\!{\sqrt[{3}]{\frac {\cos ^{5}2C}{\cos ^{2}2B}}}\!&\!+\!&\!{\sqrt[{3}]{\frac {\cos ^{5}2A}{\cos ^{2}2C}}}\!&\!=\!&\!-3\times {\frac {\sqrt[{3}]{7}}{2}}\\[2pt]{\sqrt[{3}]{\frac {\cos ^{14}2A}{\cos ^{5}2B}}}\!&\!+\!&\!{\sqrt[{3}]{\frac {\cos ^{14}2B}{\cos ^{5}2C}}}\!&\!+\!&\!{\sqrt[{3}]{\frac {\cos ^{14}2C}{\cos ^{5}2A}}}\!&\!=\!&\!0\\[2pt]{\sqrt[{3}]{\frac {\cos ^{14}2B}{\cos ^{5}2A}}}\!&\!+\!&\!{\sqrt[{3}]{\frac {\cos ^{14}2C}{\cos ^{5}2B}}}\!&\!+\!&\!{\sqrt[{3}]{\frac {\cos ^{14}2A}{\cos ^{5}2C}}}\!&\!=\!&\!-61\times {\frac {\sqrt[{3}]{7}}{8}}.\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9537ae68fa934954aeb5597d1f2df4209374a8a8)
