User:Annafitzgerald/Sandbox

Finding wavefunctions for the bound state

Solutions to the Schrödinger equation must be continuous, and continuously differentiable. These requirements are boundary conditions on the differential equations previously derived.

In this case, the finite potential well is symmetrical, so symmetry can be exploited to reduce the necessary calculations.

Summarizing the previous section:

$\psi ={\begin{cases}Fe^{-\alpha x}+Ge^{\alpha x},&{\mbox{if }}x<-L/2{\mbox{ (the region outside the box)}}\\A\sin(kx)+B\cos(kx),&{\mbox{if }}-L/2<x<L/2{\mbox{ (the region inside the box)}}\\He^{-\alpha x}+Ie^{\alpha x}&{\mbox{if }}x>L/2{\mbox{ (the region outside the box)}}\end{cases}}$

We see that as $x$ goes to $-\infty$, the $F$ term goes to infinity. Likewise, as $x$ goes to $+\infty$, the $I$ term goes to infinity. As the wave function must be finite for all $x$, this means we must set $F=I=0$, and we have:

$\psi _{1}=Ge^{\alpha x}\,\!$

and

$\psi _{3}=He^{-\alpha x}\,\!$

Next, we know that the overall $\psi \,\!$ function must be continuous and differentiable. In other words the values of the functions and their derivatives must match up at the dividing points:

$\psi _{1}(-L/2)=\psi _{2}(-L/2)\,\!$		$\psi _{2}(L/2)=\psi _{3}(L/2)\,\!$
${\frac {d\psi _{1}}{dx}}(-L/2)={\frac {d\psi _{2}}{dx}}(-L/2)\,\!$		${\frac {d\psi _{2}}{dx}}(L/2)={\frac {d\psi _{3}}{dx}}(L/2)\,\!$

These equations have two sorts of solutions, symmetric, for which $A=0$ and $G=H$, and antisymmetric, for which $B=0$ and $G=-H$. For the symmetric case we get

$He^{-\alpha L/2}=B\cos(kL/2)$

$-\alpha He^{-\alpha L/2}=-kB\sin(kL/2)$

so taking the ratio gives

$\alpha =k\tan(kL/2)$.

Similarly for the antisymmetric case we get

$\alpha =-k\cot(kL/2)$.

Recall that both $\alpha$ and $k$ depend on the energy. What we have found is that the boundary conditions cannot be satisfied for an arbitrary value of the energy. Only certain energy values, which are solutions to one or other of these two equations, are allowed. Hence we find, as always, the bound-state energies are quantized.

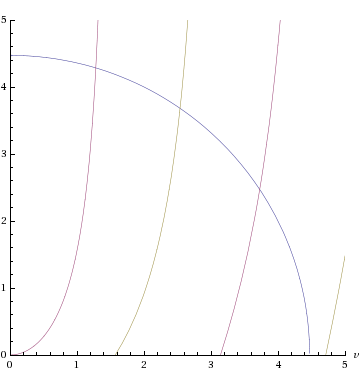
The energy equations cannot be solved analytically. Graphical or numerical solutions are aided by rewriting them a little. If we introduce the dimensionless variables $u=\alpha L/2$ and $v=kL/2$, and note from the definitions of $\alpha$ and $k$ that $u^{2}=u_{0}^{2}-v^{2}$, where $u_{0}^{2}=mL^{2}\Gamma /2\hbar ^{2}$, the master equations read

${\sqrt {u_{0}^{2}-v^{2}}}={\begin{cases}v\tan v,&{\mbox{(symmetric case) }}\\-v\cot v,&{\mbox{(antisymmetric case) }}\end{cases}}$

In the plot to the right, for $u_{0}^{2}=20$, solutions exist where the blue semi-circle intersects the purple or grey curves ($v\tan v$ and $-v\cot v$). In this case there are exactly three solutions,

$v_{1}=1.28,v_{2}=2.54$ and $v_{3}=3.73$, with the corresponding energies

$E_{n}={2\hbar ^{2}v_{n}^{2} \over mL^{2}}$.

If we want, we can go back and find the values of the constants $A,B,G,H$ in the equations now (we also need to impose the normalisation condition). On the right we show the energy levels and wave functions in this case (where $V_{0}\equiv \Gamma$ and $x_{0}\equiv \hbar /{\sqrt {2m\Gamma }}$).

We note that however small $u_{0}$ is (however shallow or narrow the well), there is always at least one bound state.

Two special cases are worth noting. As the height of the potential becomes large, $\Gamma \to \infty$, the radius of the semicircle gets larger and the roots get closer and closer to the values $v_{n}=n\pi /2$, and we recover the case of the infinite square well.

The other case is that of a very narrow, deep well - specifically the case $\Gamma \to \infty$ and $L\to 0$ with $\Gamma L$ fixed. As $u_{0}\propto \Gamma L^{2}$ it will tend to zero, and so there will only be one bound state. The approximate solution is then $v^{2}=u_{0}^{2}-u_{0}^{4}$, and the energy tends to $E=\Gamma -mL^{2}\Gamma ^{2}/2\hbar ^{2}$. But this is just the energy of the bound state of a Delta function potential of strength $\Gamma L$, as it should be.

Spherical cavity

The results above can be used to show that, contrary to the one-dimensional case, there is not always a bound state in a spherical cavity.

The ground state of a spherically symmetric potential will always have zero orbital angular momentum, and the reduced wave function $U(r)\equiv r\psi (r)$ satisfies the equation

$-{\frac {\hbar ^{2}}{2m}}{d^{2}U \over dr^{2}}+V(r)U(r)=EU(r)$

This is identical to the one-dimensional equation, except for the boundary conditions. As before, $U(r)$ and its first derivative must be continuous at the edge of the well $r=R$. However there is another condition, that $\psi (0)$ must be finite, and that requires $U(0)=0$.

By comparison with the solutions above, we can see that only the antisymmetric ones have nodes at the origin. Thus only the solutions to $\alpha =-k\cot(kR)$ are allowed. These correspond to the intersection of the semicircle with the grey curves, and so if the cavity is too shallow or small, there will be no bound state.