User:Carchasm/sandbox/Zeno
Zeno of Elea | |
|---|---|
 Zeno shows the Doors to Truth and Falsity (Veritas et Falsitas). Fresco in the Library of El Escorial, Madrid. | |
| Born | c. 495 BC |
| Died | c. 430 BC (aged around 65) Elea or Syracuse |
| Era | Pre-Socratic philosophy |
| Region | Western philosophy |
| School | Eleatic school |
Main interests | Metaphysics, ontology |
Notable ideas | Zeno's paradoxes |
Zeno of Elea (/ˈziːnoʊ ... ˈɛliə/; Ancient Greek: Ζήνων ὁ Ἐλεᾱ́της; c. 495 – c. 430 BC)[1] was a pre-Socratic Greek philosopher of Magna Graecia and a member of the Eleatic School founded by Parmenides. Aristotle called him the inventor of the dialectic.[2] He is best known for his paradoxes, which Bertrand Russell described as "immeasurably subtle and profound".[3]
Life[edit]
Little is known for certain about Zeno's life. Although written nearly a century after Zeno's death, the primary source of biographical information about Zeno is Plato's Parmenides[4] and he is also mentioned in Aristotle's Physics.[5] In the dialogue of Parmenides, Plato describes a visit to Athens by Zeno and Parmenides, at a time when Parmenides is "about 65", Zeno is "nearly 40", and Socrates is "a very young man".[6][7] Assuming an age for Socrates of around 20 and taking the date of Socrates' birth as 469 BC gives an approximate date of birth for Zeno of 490 BC. Plato says that Zeno was "tall and fair to look upon" and was "in the days of his youth … reported to have been beloved by Parmenides".[6]
Other perhaps less reliable details of Zeno's life are given by Diogenes Laërtius in his Lives and Opinions of Eminent Philosophers,[8] where it is reported that he was the son of Teleutagoras, but the adopted son of Parmenides, was "skilled to argue both sides of any question, the universal critic", and that he was arrested and perhaps killed at the hands of a tyrant of Elea.
| “ | Your noble wish, O Zeno, was to slay A cruel tyrant, freeing Elea |
” |
| — Diogenes Laërtius, Life of Zeno, the Eleatic[9][10] | ||
According to Diogenes Laërtius, Zeno conspired to overthrow Nearchus the tyrant.[11] Eventually, Zeno was arrested and tortured.[12] According to Valerius Maximus, when he was tortured to reveal the name of his colleagues in conspiracy, Zeno refused to reveal their names, although he said that he did have a secret that would be advantageous for Nearchus to hear. When Nearchus leaned in to listen to the secret, Zeno bit his ear. He "did not let go until he lost his life and the tyrant lost that part of his body."[13][14] Within Men of the Same Name, Demetrius said that the nose was bitten off instead.[15] According to the 10th-century Suda, while "Zeno was being interrogated by him, he took his own tongue between his teeth, gnawed it off, and spat it upon the tyrant", and "afterward he was thrown into a mortar and crushed and beaten to a pulp".[16][7]
Zeno may have also interacted with other tyrants. According to Laërtius, Heraclides Lembus, within his Satyrus, these events occurred against Diomedon instead of Nearchus.[11] Valerius Maximus recounts a conspiracy against the tyrant Phalaris, but this would be impossible as Phalaris had died before Zeno was even born.[14][17] According to Plutarch, Zeno attempted to kill the tyrant Demylus. After failing, he had "with his own teeth bit off his tongue, he spit it in the tyrant’s face".[18]
Works[edit]
Although many ancient writers refer to the writings of Zeno, none of his works survive intact. The main sources on the nature of Zeno's arguments on motion, in fact, come from the writings of Aristotle and Simplicius of Cilicia.[19]
Plato says that Zeno's writings were "brought to Athens for the first time on the occasion of" the visit of Zeno and Parmenides.[6] Plato also has Zeno say that this work "meant to protect the arguments of Parmenides",[6] was written in Zeno's youth, stolen, and published without his consent. Plato has Socrates paraphrase the "first thesis of the first argument" of Zeno's work as follows: "If being is many, it must be both like and unlike, and this is impossible, for neither can the like be unlike, nor the unlike like."[6]
According to Proclus in his Commentary on Plato's Parmenides, Zeno produced "not less than forty arguments revealing contradictions",[20] but only nine are now known.
Zeno's arguments are perhaps the first examples of a method of proof called reductio ad absurdum, literally meaning to reduce to the absurd. Parmenides is said[citation needed] to be the first individual to implement this style of argument. This form of argument soon became known as the epicheirema. In Book VII of his Topics, Aristotle says that an epicheirema is "a dialectical syllogism". It is a connected piece of reasoning which an opponent has put forward as true. The disputant sets out to break down the dialectical syllogism. This destructive method of argument was maintained by him to such a degree that Seneca the Younger commented a few centuries later: "If I accede to Parmenides there is nothing left but the One; if I accede to Zeno, not even the One is left."[21]
Zeno is also regarded as the first philosopher who dealt with the earliest attestable accounts of mathematical infinity.[22]
According to Sir William Smith, in the Dictionary of Greek and Roman Biography and Mythology (1870)[23]
Others content themselves with reckoning Parmenides as well as Zeno as belonging to the Pythagorean school, or with speaking of a Parraenidean life, in the same way as a Pythagorean life is spoken of; and even the censorious Timon allows Parmenides to have been a high-minded man; while Plato speaks of him with veneration, and Aristotle and others give him an unqualified preference over the rest of the Eleatics.
Eusebius quoting Aristocles of Messene says that Zeno was part of a line of philosophy that culminated in Pyrrhonism.[24]
Zeno's paradoxes[edit]
Zeno's paradoxes have puzzled, challenged, influenced, inspired, infuriated, and amused philosophers, mathematicians, and physicists for over two millennia. The most famous are the arguments against motion described by Aristotle in his Physics, Book VI.[25]
-
Achilles and the tortoise
-
The dichotomy
-
The arrow
-
The moving rows
Zeno's paradoxes are a set of philosophical problems generally thought to have been devised by Greek philosopher Zeno of Elea (c. 490–430 BC) to support Parmenides' doctrine that contrary to the evidence of one's senses, the belief in plurality and change is mistaken, and in particular that motion is nothing but an illusion. It is usually assumed, based on Plato's Parmenides (128a–d), that Zeno took on the project of creating these paradoxes because other philosophers had created paradoxes against Parmenides' view. Thus Plato has Zeno say the purpose of the paradoxes "is to show that their hypothesis that existences are many, if properly followed up, leads to still more absurd results than the hypothesis that they are one."[26] Plato has Socrates claim that Zeno and Parmenides were essentially arguing exactly the same point.[27] Some of Zeno's nine surviving paradoxes (preserved in Aristotle's Physics[28][29]and Simplicius's commentary thereon) are essentially equivalent to one another. Aristotle offered a refutation of some of them.[28] Three of the strongest and most famous—that of Achilles and the tortoise, the Dichotomy argument, and that of an arrow in flight—are presented in detail below. Zeno's arguments are perhaps the first examples of a method of proof called reductio ad absurdum, also known as proof by contradiction. They are also credited as a source of the dialectic method used by Socrates.[30] Some mathematicians and historians, such as Carl Boyer, hold that Zeno's paradoxes are simply mathematical problems, for which modern calculus provides a mathematical solution.[31] Some philosophers, however, say that Zeno's paradoxes and their variations (see Thomson's lamp) remain relevant metaphysical problems.[32][33][34] The origins of the paradoxes are somewhat unclear. Diogenes Laërtius, a fourth source for information about Zeno and his teachings, citing Favorinus, says that Zeno's teacher Parmenides was the first to introduce the paradox of Achilles and the tortoise. But in a later passage, Laërtius attributes the origin of the paradox to Zeno, explaining that Favorinus disagrees.[35]
Dichotomy paradox[edit]
That which is in locomotion must arrive at the half-way stage before it arrives at the goal.
Suppose Atalanta wishes to walk to the end of a path. Before she can get there, she must get halfway there. Before she can get halfway there, she must get a quarter of the way there. Before traveling a quarter, she must travel one-eighth; before an eighth, one-sixteenth; and so on.


The resulting sequence can be represented as:
This description requires one to complete an infinite number of tasks, which Zeno maintains is an impossibility.[36]
This sequence also presents a second problem in that it contains no first distance to run, for any possible (finite) first distance could be divided in half, and hence would not be first after all. Hence, the trip cannot even begin. The paradoxical conclusion then would be that travel over any finite distance can be neither completed nor begun, and so all motion must be an illusion.[37]
This argument is called the "Dichotomy" because it involves repeatedly splitting a distance into two parts. An example with the original sense can be found in an asymptote. It is also known as the Race Course paradox.
Achilles and the tortoise[edit]

In a race, the quickest runner can never overtake the slowest, since the pursuer must first reach the point whence the pursued started, so that the slower must always hold a lead.
In the paradox of Achilles and the tortoise, Achilles is in a footrace with the tortoise. Achilles allows the tortoise a head start of 100 meters, for example. Suppose that each racer starts running at some constant speed, one faster than the other. After some finite time, Achilles will have run 100 meters, bringing him to the tortoise's starting point. During this time, the tortoise has run a much shorter distance, say 2 meters. It will then take Achilles some further time to run that distance, by which time the tortoise will have advanced farther; and then more time still to reach this third point, while the tortoise moves ahead. Thus, whenever Achilles arrives somewhere the tortoise has been, he still has some distance to go before he can even reach the tortoise. As Aristotle noted, this argument is similar to the Dichotomy.[38] It lacks, however, the apparent conclusion of motionlessness.
Arrow paradox[edit]
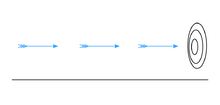
If everything when it occupies an equal space is at rest at that instant of time, and if that which is in locomotion is always occupying such a space at any moment, the flying arrow is therefore motionless at that instant of time and at the next instant of time but if both instants of time are taken as the same instant or continuous instant of time then it is in motion.[39]
In the arrow paradox, Zeno states that for motion to occur, an object must change the position which it occupies. He gives an example of an arrow in flight. He states that in any one (duration-less) instant of time, the arrow is neither moving to where it is, nor to where it is not.[40]
It cannot move to where it is not, because no time elapses for it to move there; it cannot move to where it is, because it is already there. In other words, at every instant of time there is no motion occurring. If everything is motionless at every instant, and time is entirely composed of instants, then motion is impossible. Whereas the first two paradoxes divide space, this paradox starts by dividing time—and not into segments, but into points.[41]
Paradox of place[edit]
From Aristotle:
If everything that exists has a place, place too will have a place, and so on ad infinitum.[42]
Paradox of the grain of millet[edit]
Description of the paradox from the Routledge Dictionary of Philosophy:
The argument is that a single grain of millet makes no sound upon falling, but a thousand grains make a sound. Hence a thousand nothings become something, an absurd conclusion.[43]
Aristotle's refutation:
Zeno is wrong in saying that there is no part of the millet that does not make a sound: for there is no reason why any such part should not in any length of time fail to move the air that the whole bushel moves in falling. In fact it does not of itself move even such a quantity of the air as it would move if this part were by itself: for no part even exists otherwise than potentially.[44]
Description from Nick Huggett:
This is a Parmenidean argument that one cannot trust one's sense of hearing. Aristotle's response seems to be that even inaudible sounds can add to an audible sound.[45]
The moving rows (or stadium)[edit]

From Aristotle:
... concerning the two rows of bodies, each row being composed of an equal number of bodies of equal size, passing each other on a race-course as they proceed with equal velocity in opposite directions, the one row originally occupying the space between the goal and the middle point of the course and the other that between the middle point and the starting-post. This...involves the conclusion that half a given time is equal to double that time.[46]
For an expanded account of Zeno's arguments as presented by Aristotle, see Simplicius's commentary On Aristotle's Physics.[full citation needed]
Similar Chinese paradoxes[edit]

Roughly contemporaneously during the Warring States period (475–221 BCE), ancient Chinese philosophers from the School of Names, a school of thought similarly concerned with logic and dialectics, developed paradoxes similar to those of Zeno. The works of the School of Names have largely been lost, with the exception of portions of the Gongsun Longzi. The second of the Ten Theses of Hui Shi suggests knowledge of infinitesimals: That which has no thickness cannot be piled up; yet it is a thousand li in dimension.
Among the many puzzles recorded in his Zhuangzi is one very similar to Zeno's Dichotomy:
"If from a stick a foot long you every day take the half of it, in a myriad ages it will not be exhausted."
— Zhuangzi, chapter 33 (Legge translation)[47]
The Mohist canon appears to propose a solution to this paradox by arguing that in moving across a measured length, the distance is not covered in successive fractions of the length, but in one stage. Due to the lack of surviving works from the School of Names, most of the other paradoxes listed are difficult to interpret.[48]
Proposed solutions[edit]
According to Simplicius, Diogenes the Cynic said nothing upon hearing Zeno's arguments, but stood up and walked, in order to demonstrate the falsity of Zeno's conclusions (see solvitur ambulando). To fully solve any of the paradoxes, however, one needs to show what is wrong with the argument, not just the conclusions. Through history, several solutions have been proposed, among the earliest recorded being those of Aristotle and Archimedes.
Aristotle[edit]
Aristotle (384 BC−322 BC) remarked that as the distance decreases, the time needed to cover those distances also decreases, so that the time needed also becomes increasingly small.[49][failed verification][50] Aristotle also distinguished "things infinite in respect of divisibility" (such as a unit of space that can be mentally divided into ever smaller units while remaining spatially the same) from things (or distances) that are infinite in extension ("with respect to their extremities").[51]Aristotle's objection to the arrow paradox was that "Time is not composed of indivisible nows any more than any other magnitude is composed of indivisibles."[52]Thomas Aquinas, commenting on Aristotle's objection, wrote "Instants are not parts of time, for time is not made up of instants any more than a magnitude is made of points, as we have already proved. Hence it does not follow that a thing is not in motion in a given time, just because it is not in motion in any instant of that time."[53]
Archimedes[edit]
Before 212 BC, Archimedes had developed a method to derive a finite answer for the sum of infinitely many terms that get progressively smaller. (See: Geometric series, 1/4 + 1/16 + 1/64 + 1/256 + · · ·, The Quadrature of the Parabola.) His argument, applying the method of exhaustion to prove that the infinite sum in question is equal to the area of a particular square, is largely geometric but quite rigorous. Today's analysis achieves the same result, using limits (see convergent series). These methods allow the construction of solutions based on the conditions stipulated by Zeno, i.e. the amount of time taken at each step is geometrically decreasing.[31][54]
Paradoxes in modern times[edit]
Infinite processes remained theoretically troublesome in mathematics until the late 19th century. With the epsilon-delta definition of limit, Weierstrass and Cauchy developed a rigorous formulation of the logic and calculus involved. These works resolved the mathematics involving infinite processes.[55][56] A humorous take is offered by Tom Stoppard in his 1972 play Jumpers, in which the principal protagonist, the philosophy professor George Moore, suggests that according to Zeno's paradox, Saint Sebastian, a 3rd Century Christian saint martyred by being shot with arrows, died of fright.
While mathematics can calculate where and when the moving Achilles will overtake the Tortoise of Zeno's paradox, philosophers such as Kevin Brown[32] and Francis Moorcroft[33] claim that mathematics does not address the central point in Zeno's argument, and that solving the mathematical issues does not solve every issue the paradoxes raise.
Popular literature often misrepresents Zeno's arguments. For example, Zeno is often said to have argued that the sum of an infinite number of terms must itself be infinite–with the result that not only the time, but also the distance to be travelled, become infinite.[57] However, none of the original ancient sources has Zeno discussing the sum of any infinite series. Simplicius has Zeno saying "it is impossible to traverse an infinite number of things in a finite time". This presents Zeno's problem not with finding the sum, but rather with finishing a task with an infinite number of steps: how can one ever get from A to B, if an infinite number of (non-instantaneous) events can be identified that need to precede the arrival at B, and one cannot reach even the beginning of a "last event"?[32][33][34][58]
Debate continues on the question of whether or not Zeno's paradoxes have been resolved.[citation needed] In The History of Mathematics: An Introduction (2010) Burton writes, "Although Zeno's argument confounded his contemporaries, a satisfactory explanation incorporates a now-familiar idea, the notion of a 'convergent infinite series.'"[59]
Lewis Carroll and Douglas Hofstadter[edit]
What the Tortoise Said to Achilles,[60] written in 1895 by Lewis Carroll, was an attempt to reveal an analogous paradox in the realm of pure logic. If Carroll's argument is valid, the implication is that Zeno's paradoxes of motion are not essentially problems of space and time, but go right to the heart of reasoning itself.[citation needed] Douglas Hofstadter made Carroll's article a centrepiece of his book Gödel, Escher, Bach: An Eternal Golden Braid, writing many more dialogues between Achilles and the Tortoise to elucidate his arguments. Hofstadter connects Zeno's paradoxes to Gödel's incompleteness theorem in an attempt to demonstrate that the problems raised by Zeno are pervasive and manifest in formal systems theory, computing and the philosophy of mind.[citation needed]
Bertrand Russell[edit]
Bertrand Russell offered what is known as the "at-at theory of motion". It agrees that there can be no motion "during" a durationless instant, and contends that all that is required for motion is that the arrow be at one point at one time, at another point another time, and at appropriate points between those two points for intervening times. In this view motion is just change in position over time.[61][62]Bertrand Russell offered a "solution" to the paradoxes based on the work of Georg Cantor,[63] but Brown concludes "Given the history of 'final resolutions', from Aristotle onwards, it's probably foolhardy to think we've reached the end. It may be that Zeno's arguments on motion, because of their simplicity and universality, will always serve as a kind of 'Rorschach image' onto which people can project their most fundamental phenomenological concerns (if they have any)."[32]
Hermann Weyl[edit]
Another proposed solution is to question one of the assumptions Zeno used in his paradoxes (particularly the Dichotomy), which is that between any two different points in space (or time), there is always another point. Without this assumption there are only a finite number of distances between two points, hence there is no infinite sequence of movements, and the paradox is resolved. According to Hermann Weyl, the assumption that space is made of finite and discrete units is subject to a further problem, given by the "tile argument" or "distance function problem".[64][65]According to this, the length of the hypotenuse of a right angled triangle in discretized space is always equal to the length of one of the two sides, in contradiction to geometry. Jean Paul Van Bendegem has argued that the Tile Argument can be resolved, and that discretization can therefore remove the paradox.[31][66]
Philosophy of time[edit]
An alternative conclusion, proposed by Henri Bergson in his 1896 book Matter and Memory, is that, while the path is divisible, the motion is not.[67] In this argument, instants in time and instantaneous magnitudes do not physically exist. An object in relative motion cannot have an instantaneous or determined relative position, and so cannot have its motion fractionally dissected. In 2003, Peter Lynds put forth a very similar argument: all of Zeno's motion paradoxes are resolved by the conclusion that instants in time and instantaneous magnitudes do not physically exist.[68][69][70][71] Lynds argues that an object in relative motion cannot have an instantaneous or determined relative position (for if it did, it could not be in motion), and so cannot have its motion fractionally dissected as if it does, as is assumed by the paradoxes. For more about the inability to know both speed and location, see Heisenberg uncertainty principle. Nick Huggett argues that Zeno is assuming the conclusion when he says that objects that occupy the same space as they do at rest must be at rest.[41]
Quantum Zeno effect[edit]
In 1977,[72] physicists E. C. George Sudarshan and B. Misra discovered that the dynamical evolution (motion) of a quantum system can be hindered (or even inhibited) through observation of the system.[73] This effect is usually called the "quantum Zeno effect" as it is strongly reminiscent of Zeno's arrow paradox. This effect was first theorized in 1958.[74]
Zeno behaviour[edit]
In the field of verification and design of timed and hybrid systems, the system behaviour is called Zeno if it includes an infinite number of discrete steps in a finite amount of time.[75] Some formal verification techniques exclude these behaviours from analysis, if they are not equivalent to non-Zeno behaviour.[76][77] In systems design these behaviours will also often be excluded from system models, since they cannot be implemented with a digital controller.[78]
See also[edit]
- Incommensurable magnitudes – Number that is not a ratio of integers
- List of speakers in Plato's dialogues
- Infinite regress
- Philosophy of space and time
- Renormalization
- Ross–Littlewood paradox
- School of Names
- Supertask
- "What the Tortoise Said to Achilles", an allegorical dialogue on the foundations of logic by Lewis Carroll (1895).
- Zeno machine
- List of Paradoxes
Notes[edit]
- ^ Zeno of Elea - Greek philosopher and mathematician.
- ^ Diogenes Laërtius, 8.57, 9.25
- ^ Russell (1996 [1903]), p. 347: "In this capricious world nothing is more capricious than posthumous fame. One of the most notable victims of posterity's lack of judgment is the Eleatic Zeno. Having invented four arguments all immeasurably subtle and profound, the grossness of subsequent philosophers pronounced him to be a mere ingenious juggler, and his arguments to be one and all sophisms. After two thousand years of continual refutation, these sophisms were reinstated and made the foundation of a mathematical renaissance..."
- ^ Plato (c. 380 – 367 BC). Parmenides, translated by Benjamin Jowett. Internet Classics Archive.
- ^ Aristotle (c. mid 4th century BC), Physics 233a and 239b.
- ^ a b c d e Plato, Parmenides 127b–e.
- ^ a b "Suda, Zeno of Elea". Suda On Line: Byzantine Lexicography. Stoa Consortium. Archived from the original on September 17, 2019. (at footnote n. 2)
- ^ Diogenes Laërtius. The Lives and Opinions of Eminent Philosophers, translated by C. D. Yonge. London: Henry G. Bohn, 1853. Scanned and edited for Peithô's Web Archived 2010-12-12 at the Wayback Machine.
- ^ "The paradox ideas of Zeno of Elea, is motion an illusion or even impossible?". Archived from the original on 2015-06-07. Retrieved 2015-04-12.
- ^ "Diogenes Laertius, Lives of Eminent Philosophers, Book IX, Chapter 5. Zeno of Elea".
- ^ a b Diogenes Laërtius, Lives of Eminent Philosophers. Book IX.5.26.
- ^ Boethius, The Consolation of Philosophy. Book 1.III.
- ^ Valerius Maximus, Memorable Deeds and Sayings. Foreign Stories 3. ext. 3.
- ^ a b Maximus, Valerius; Walker, Henry J. (2004). Memorable Deeds and Sayings: One Thousand Tales from Ancient Rome. Hackett Pub. p. 97. ISBN 978-0-87220-674-8.
- ^ Diogenes Laërtius, Lives of Eminent Philosophers. Book IX.5.27.
- ^ "Zeno of Elea". Suda. Topostext.org. Archived from the original on January 24, 2019. Retrieved June 11, 2021.
- ^ Valerius Maximus, Memorable Deeds and Sayings. Foreign Stories 3. ext. 2.
- ^ Plutarch, Against Colotes.
- ^ Cajori, Florian (1920). "The Purpose of Zeno's Arguments on Motion". Isis. 3 (1): 7–20. doi:10.1086/357889.
- ^ Proclus, Commentary on Plato's Parmenides, p. 29.
- ^ Zeno in The Presocratics, Philip Wheelwright ed., The Odyssey Press, 1966, pp. 106–107.
- ^ Boyer, Carl B.; Merzbach, Uta C. (2011). A History of Mathematics (Third ed.). Hoboken, New Jersey: John Wiley & Sons. p. 538. ISBN 978-0-470-52548-7.
Ever since the days of Zeno, men had been talking about infinity,...
- ^
 Smith, William, ed. (1870). "Parmenides". Dictionary of Greek and Roman Biography and Mythology. p. 125.
Smith, William, ed. (1870). "Parmenides". Dictionary of Greek and Roman Biography and Mythology. p. 125.
- ^ Eusebius, Praeparatio Evangelica Chapter XVII
- ^ Aristotle. Physics, translated by R.P. Hardie and R.K. Gaye. Internet Classics Archive.
- ^ Parmenides 128d
- ^ Parmenides 128a–b
- ^ a b Aristotle's Physics "Physics" by Aristotle translated by R. P. Hardie and R. K. Gaye
- ^ "Greek text of "Physics" by Aristotle (refer to §4 at the top of the visible screen area)". Archived from the original on 2008-05-16.
- ^ ([fragment 65], Diogenes Laërtius. IX Archived 2010-12-12 at the Wayback Machine 25ff and VIII 57).
- ^ a b c Boyer, Carl (1959). The History of the Calculus and Its Conceptual Development. Dover Publications. p. 295. ISBN 978-0-486-60509-8. Retrieved 2010-02-26.
If the paradoxes are thus stated in the precise mathematical terminology of continuous variables (...) the seeming contradictions resolve themselves.
- ^ a b c d Brown, Kevin. "Zeno and the Paradox of Motion". Reflections on Relativity. Archived from the original on 2012-12-05. Retrieved 2010-06-06.
- ^ a b c Moorcroft, Francis. "Zeno's Paradox". Archived from the original on 2010-04-18.
- ^ a b Papa-Grimaldi, Alba (1996). "Why Mathematical Solutions of Zeno's Paradoxes Miss the Point: Zeno's One and Many Relation and Parmenides' Prohibition" (PDF). The Review of Metaphysics. 50: 299–314.
- ^ Diogenes Laërtius, Lives, 9.23 and 9.29.
- ^ Lindberg, David (2007). The Beginnings of Western Science (2nd ed.). University of Chicago Press. p. 33. ISBN 978-0-226-48205-7.
- ^ Huggett, Nick (2010). "Zeno's Paradoxes: 3.1 The Dichotomy". Stanford Encyclopedia of Philosophy. Retrieved 2011-03-07.
- ^ Huggett, Nick (2010). "Zeno's Paradoxes: 3.2 Achilles and the Tortoise". Stanford Encyclopedia of Philosophy. Retrieved 2011-03-07.
- ^ Aristotle. "Physics". The Internet Classics Archive.
Zeno's reasoning, however, is fallacious, when he says that if everything when it occupies an equal space is at rest, and if that which is in locomotion is always occupying such a space at any moment, the flying arrow is therefore motionless. This is false, for time is not composed of indivisible moments any more than any other magnitude is composed of indivisibles.
- ^ Laërtius, Diogenes (c. 230). "Pyrrho". Lives and Opinions of Eminent Philosophers. Vol. IX. passage 72. ISBN 1-116-71900-2.
- ^ a b Huggett, Nick (2010). "Zeno's Paradoxes: 3.3 The Arrow". Stanford Encyclopedia of Philosophy. Retrieved 2011-03-07.
- ^ Aristotle Physics IV:1, 209a25
- ^ The Michael Proudfoot, A.R. Lace. Routledge Dictionary of Philosophy. Routledge 2009, p. 445
- ^ Aristotle Physics VII:5, 250a20
- ^ Huggett, Nick, "Zeno's Paradoxes", The Stanford Encyclopedia of Philosophy (Winter 2010 Edition), Edward N. Zalta (ed.), http://plato.stanford.edu/entries/paradox-zeno/#GraMil
- ^ Aristotle Physics VI:9, 239b33
- ^ Müller, Max, ed. (1891). "The Writings of Kwang Tse". Sacred Books of the East. Vol. 40. Translated by Legge, James. Oxford University Press.
- ^ "School of Names > Miscellaneous Paradoxes (Stanford Encyclopedia of Philosophy)". plato.stanford.edu. Retrieved 2020-01-30.
- ^ Aristotle. Physics 6.9
- ^ Aristotle's observation that the fractional times also get shorter does not guarantee, in every case, that the task can be completed. One case in which it does not hold is that in which the fractional times decrease in a harmonic series, while the distances decrease geometrically, such as: 1/2 s for 1/2 m gain, 1/3 s for next 1/4 m gain, 1/4 s for next 1/8 m gain, 1/5 s for next 1/16 m gain, 1/6 s for next 1/32 m gain, etc. In this case, the distances form a convergent series, but the times form a divergent series, the sum of which has no limit. [original research?] Archimedes developed a more explicitly mathematical approach than Aristotle.
- ^ Aristotle. Physics 6.9; 6.2, 233a21-31
- ^ Aristotle. Physics. Vol. VI. Part 9 verse: 239b5. ISBN 0-585-09205-2.
- ^ Aquinas. Commentary on Aristotle's Physics, Book 6.861
- ^ George B. Thomas, Calculus and Analytic Geometry, Addison Wesley, 1951
- ^ Lee, Harold (1965). "Are Zeno's Paradoxes Based on a Mistake?". Mind. 74 (296). Oxford University Press: 563–570. doi:10.1093/mind/LXXIV.296.563. JSTOR 2251675.
- ^ B Russell (1956) Mathematics and the metaphysicians in "The World of Mathematics" (ed. J R Newman), pp 1576-1590.
- ^ Benson, Donald C. (1999). The Moment of Proof : Mathematical Epiphanies. New York: Oxford University Press. p. 14. ISBN 978-0195117219.
- ^ Huggett, Nick (2010). "Zeno's Paradoxes: 5. Zeno's Influence on Philosophy". Stanford Encyclopedia of Philosophy. Retrieved 2011-03-07.
- ^ Burton, David, A History of Mathematics: An Introduction, McGraw Hill, 2010, ISBN 978-0-07-338315-6
- ^ Carroll, Lewis (1895-04-01). "What the Tortoise Said to Achilles". Mind. IV (14): 278–280. doi:10.1093/mind/IV.14.278. ISSN 0026-4423.
- ^ Huggett, Nick (1999). Space From Zeno to Einstein. ISBN 0-262-08271-3.
- ^ Salmon, Wesley C. (1998). Causality and Explanation. p. 198. ISBN 978-0-19-510864-4.
- ^ Russell, Bertrand (2002) [First published in 1914 by The Open Court Publishing Company]. "Lecture 6. The Problem of Infinity Considered Historically". Our Knowledge of the External World: As a Field for Scientific Method in Philosophy. Routledge. p. 169. ISBN 0-415-09605-7.
- ^ Van Bendegem, Jean Paul (17 March 2010). "Finitism in Geometry". Stanford Encyclopedia of Philosophy. Retrieved 2012-01-03.
- ^ Cohen, Marc (11 December 2000). "ATOMISM". History of Ancient Philosophy, University of Washington. Archived from the original on July 12, 2010. Retrieved 2012-01-03.
- ^ van Bendegem, Jean Paul (1987). "Discussion:Zeno's Paradoxes and the Tile Argument". Philosophy of Science. 54 (2). Belgium: 295–302. doi:10.1086/289379. JSTOR 187807. S2CID 224840314.
- ^ Bergson, Henri (1896). Matière et Mémoire [Matter and Memory] (PDF). Translation 1911 by Nancy Margaret Paul & W. Scott Palmer. George Allen and Unwin. pp. 77–78 of the PDF.
- ^ "Zeno's Paradoxes: A Timely Solution". January 2003.
- ^ Lynds, Peter. Time and Classical and Quantum Mechanics: Indeterminacy vs. Discontinuity. Foundations of Physics Letter s (Vol. 16, Issue 4, 2003). doi:10.1023/A:1025361725408
- ^ Time’s Up, Einstein, Josh McHugh, Wired Magazine, June 2005
- ^ S E Robbins (2004) On time, memory and dynamic form. Consciousness and Cognition 13(4), 762-788: "Lynds, his reviewers and consultants (e.g., J.J.C. Smart) are apparently unaware of his total precedence by Bergson"
- ^ Sudarshan, E. C. G.; Misra, B. (1977). "The Zeno's paradox in quantum theory" (PDF). Journal of Mathematical Physics. 18 (4): 756–763. Bibcode:1977JMP....18..756M. doi:10.1063/1.523304. OSTI 7342282.
- ^ W.M.Itano; D.J. Heinsen; J.J. Bokkinger; D.J. Wineland (1990). "Quantum Zeno effect" (PDF). Physical Review A. 41 (5): 2295–2300. Bibcode:1990PhRvA..41.2295I. doi:10.1103/PhysRevA.41.2295. PMID 9903355. Archived from the original (PDF) on 2004-07-20. Retrieved 2004-07-23.
- ^ Khalfin, L.A. (1958). "Contribution to the Decay Theory of a Quasi-Stationary State". Soviet Phys. JETP. 6: 1053. Bibcode:1958JETP....6.1053K.
- ^ Paul A. Fishwick, ed. (1 June 2007). "15.6 "Pathological Behavior Classes" in chapter 15 "Hybrid Dynamic Systems: Modeling and Execution" by Pieter J. Mosterman, The Mathworks, Inc.". Handbook of dynamic system modeling. Chapman & Hall/CRC Computer and Information Science (hardcover ed.). Boca Raton, Florida, USA: CRC Press. pp. 15–22 to 15–23. ISBN 978-1-58488-565-8. Retrieved 2010-03-05.
- ^ Lamport, Leslie (2002). Specifying Systems (PDF). Addison-Wesley. p. 128. ISBN 0-321-14306-X. Retrieved 2010-03-06.
{{cite book}}:|journal=ignored (help) - ^ Zhang, Jun; Johansson, Karl; Lygeros, John; Sastry, Shankar (2001). "Zeno hybrid systems" (PDF). International Journal for Robust and Nonlinear Control. 11 (5): 435. doi:10.1002/rnc.592. S2CID 2057416. Archived from the original (PDF) on August 11, 2011. Retrieved 2010-02-28.
- ^ Franck, Cassez; Henzinger, Thomas; Raskin, Jean-Francois (2002). "A Comparison of Control Problems for Timed and Hybrid Systems". Archived from the original on May 28, 2008. Retrieved 2010-03-02.
{{cite journal}}: Cite journal requires|journal=(help)
References[edit]
- Kirk, G. S., J. E. Raven, M. Schofield (1984) The Presocratic Philosophers: A Critical History with a Selection of Texts, 2nd ed. Cambridge University Press. ISBN 0-521-27455-9.
- Huggett, Nick (2010). "Zeno's Paradoxes". Stanford Encyclopedia of Philosophy. Retrieved 2011-03-07.
- Plato (1926) Plato: Cratylus. Parmenides. Greater Hippias. Lesser Hippias, H. N. Fowler (Translator), Loeb Classical Library. ISBN 0-674-99185-0.
- Sainsbury, R.M. (2003) Paradoxes, 2nd ed. Cambridge University Press. ISBN 0-521-48347-6.
- Skyrms, Brian (1983). "Zeno's Paradox of Measure". In Cohen, R. S.; Laudan, L. (eds.). Physics, Philosphy, and Psychoanalysis. Dordrecht: Reidel. pp. 223–254. ISBN 90-277-1533-5.
- Plato; Fowler, Harold North (1925) [1914]. Plato in twelve volumes. 8, The Statesman.(Philebus).(Ion). Loeb Classical Library. trans. W. R. M. Lamb. Cambridge, Massachusetts: Harvard U.P. ISBN 978-0-434-99164-8. OCLC 222336129.
- Proclus; Morrow, Glenn R.; Dillon, John M. (1992) [1987]. Proclus' Commentary on Plato's Parmenides. Princeton, N.J.: Princeton University Press. ISBN 978-0-691-02089-1. OCLC 27251522.
- Russell, Bertrand (1996) [1903]. The Principles of Mathematics. New York, NY: Norton. ISBN 978-0-393-31404-5. OCLC 247299160.
- Hornschemeier, Paul (2007). The Three Paradoxes. Seattle, WA: Fantagraphics Books.
Further reading[edit]
- Barnes, Jonathan. 1982. The Presocratic Philosophers. 2d ed. London: Routledge & Kegan Paul.
- Lewis, Eric. 1999. "The Dogmas of Indivisibility: On the Origins of Ancient Atomism. In Proceedings of the Boston Area Colloquium in Ancient Philosophy. Vol. 14. Edited by John J. Cleary and Gary M. Gurtler, S. J., 1–21. Leiden, The Netherlands: Brill.
- McKirahan, Richard. 2001. "Zeno’s Dichotomy in Aristotle." Philosophical Inquiry 23.1–2: 1–24.
- Navia, Luis. E. 1993. The Presocratic Philosophers: An Annotated Bibliography. New York and London: Garland.
- Owen, G. E. L. 1958. "Zeno and the Mathematicians." Proceedings of the Aristotelian Society 58:199–222.
- Papa-Grimaldi, Alba. 1996. "Why Mathematical Solutions of Zeno’s Paradoxes Miss the Point: Zeno’s One and many Relation and Parmenides’ Prohibition." Review of Metaphysics 50.2: 299–314.
- Sainsbury, Mark. 1988. Paradoxes. Cambridge: Cambridge University Press.
- Salmon, Wesley C., ed. 1970. Zeno’s Paradoxes. Indianapolis, IN, and New York: Bobbs-Merrill.
- Vlastos, Gregory. 1967. "Zeno of Elea." In The Encyclopedia of Philosophy. Vol. 8. Edited by Paul Edwards, 369–379. New York and London: Macmillan.
- White, Michael J. 1992. The Continuous and the Discrete: Ancient Physical Theories from a Contemporary Perspective. Oxford: Clarendon.
External links[edit]
 Media related to Carchasm/sandbox/Zeno at Wikimedia Commons
Media related to Carchasm/sandbox/Zeno at Wikimedia Commons Works related to Zeno at Wikisource
Works related to Zeno at Wikisource Quotations related to Carchasm/sandbox/Zeno at Wikiquote
Quotations related to Carchasm/sandbox/Zeno at Wikiquote
- O'Connor, John J.; Robertson, Edmund F., "Carchasm/sandbox/Zeno", MacTutor History of Mathematics Archive, University of St Andrews
- Zeno's Paradoxes
- "Antinomy", Encyclopedia of Mathematics, EMS Press, 2001 [1994]
- Palmer, John. "Zeno of Elea". In Zalta, Edward N. (ed.). Stanford Encyclopedia of Philosophy.
- Introduction to Mathematical Philosophy, Ludwig-Maximilians-Universität München
- Silagadze, Z. K. "Zeno meets modern science,"
- Zeno's Paradox: Achilles and the Tortoise by Jon McLoone, Wolfram Demonstrations Project.
- Kevin Brown on Zeno and the Paradox of Motion
- Palmer, John. "Zeno of Elea". In Zalta, Edward N. (ed.). Stanford Encyclopedia of Philosophy.
- This article incorporates material from Zeno's paradox on PlanetMath, which is licensed under the Creative Commons Attribution/Share-Alike License.
- Grime, James. "Zeno's Paradox". Numberphile. Brady Haran. Archived from the original on 2018-10-03. Retrieved 2013-04-13.
- Plato's Parmenides.
- Aristotle's Physics.
 Laërtius, Diogenes (1925). . Lives of the Eminent Philosophers. Vol. 2:9. Translated by Hicks, Robert Drew (Two volume ed.). Loeb Classical Library.
Laërtius, Diogenes (1925). . Lives of the Eminent Philosophers. Vol. 2:9. Translated by Hicks, Robert Drew (Two volume ed.). Loeb Classical Library.- Fragments of Zeno





