User:Tomruen/List of Coxeter groups
This test article is my attempt to construct Coxeter groups by rank, including products. I subdivide them by their finite order, infinite, or hyperbolic infinite.
I name them by their group names, Coxeter's bracket notation names, and their Coxeter-Dynkin diagram graphs. I also give an example polytope or tessellation that has this symmetry.
Finite Definite (spherical)[edit]
Rank 1[edit]
(1-space)
Rank 2[edit]
(2-space)
(2-space prismatic)
- A1xA1: [ ]x[ ]


 =
= 

 (rectangle)
(rectangle)
Rank 3[edit]
(3-space)
- A3: [3,3]




 (tetrahedron)
(tetrahedron) - B3: [4,3]




 (cube/octahedron)
(cube/octahedron) - H3: [5,3]

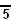


 (dodecahedron/icosahedron)
(dodecahedron/icosahedron)
(3-space prismatic)
- I2(p)xA1: [p]x[ ]

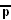


 (p-gonal prism)
(p-gonal prism) - A1xA1xA1: [ ]x[ ]x[ ]




 =
= 



 (cube/cuboid)
(cube/cuboid)
Rank 4[edit]
(4-space)
- A4: [3,3,3]






 (5-cell)
(5-cell) - B4: [4,3,3]






 (tesseract/16-cell)
(tesseract/16-cell) - D4: [31,1,1]




 (24-cell)
(24-cell) - F4: [3,4,3]






 (24-cell)
(24-cell) - H4: [5,3,3]

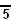




 (120-cell/600-cell)
(120-cell/600-cell)
(4-space prismatic)
- A3xA1: [3,3]x[ ]






 (tetrahedral prism)
(tetrahedral prism) - B3xA1: [4,3]x[ ]






 (tesseract/orthoplex)
(tesseract/orthoplex) - H3xA1: [5,3]x[ ]

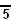




 (dodecahedral prism)
(dodecahedral prism) - I2(p)xA1xA1: [p]x[ ]x[ ]

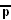




 =
= 
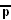




 (p-4 duoprism)
(p-4 duoprism) - A1xA1xA1xA1: [ ]x[ ]x[ ]x[ ]






 =
= 





 (tesseract/orthoplex)
(tesseract/orthoplex) - I2(p)xI2(q) [p]x[q]

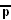



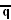
 (p-q duoprism)
(p-q duoprism)
Rank 5[edit]
(5-space)
- A5: [3,3,3,3]








 (hexateron)
(hexateron) - B5: [4,3,3,3]








 (Penteract)
(Penteract) - D5: [32,1,1]






 (Demipenteract)
(Demipenteract)
(5-space prismatic)
- A4xA1: [3,3,3]x[ ]









- B4xA1: [4,3,3]x[ ] -









- F4xA1: [3,4,3]x[ ] -









- H4xA1: [5,3,3]x[ ] -

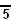







- D4xA1: [31,1,1]x[ ] -







- A3xI2p: [3,3]x[p] -







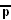

- B3xI2p: [4,3]x[p] -







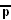

- H3xI2p: [5,3]x[p] -

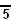





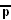

- I2pxI2qxA1: [p]x[q]x[ ] -

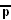



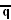



Rank 6[edit]
(6-space)
- A6: [3,3,3,3,3]










 (6-simplex)
(6-simplex) - B6: [4,3,3,3,3]










 (6-orthoplex/6-hypercube)
(6-orthoplex/6-hypercube) - D6: [33,1,1]








 (6-orthoplex)
(6-orthoplex) - E6: [32,2,1]








 (1_22 polytope)
(1_22 polytope)
Uniform prism
There are 6 categorical uniform prisms based the uniform 5-polytopes.
| # | Coxeter group | Coxeter-Dynkin diagram | |
|---|---|---|---|
| 1 | A5×A1 | [3,3,3,3] × [ ] | |
| 2 | B5×A1 | [4,3,3,3] × [ ] | |
| 3 | D5×A1 | [32,1,1] × [ ] | |
| # | Coxeter group | Coxeter-Dynkin diagram | |
|---|---|---|---|
| 4 | A3×I2(p)×A1 | [3,3] × [p] × [ ] | |
| 5 | B3×I2(p)×A1 | [4,3] × [p] × [ ] | |
| 6 | H3×I2(p)×A1 | [5,3] × [p] × [ ] | |
Uniform duoprism
There are 11 categorical uniform duoprismatic families of polytopes based on Cartesian products of lower dimensional uniform polytopes. Five are formed as the product of a uniform polychoron with a regular polygon, and six are formed by the product of two uniform polyhedra:
| # | Coxeter group | Coxeter-Dynkin diagram | |
|---|---|---|---|
| 1 | A4×I2(p) | [3,3,3] × [p] | |
| 2 | B4×I2(p) | [4,3,3] × [p] | |
| 3 | F4×I2(p) | [3,4,3] × [p] | |
| 4 | H4×I2(p) | [5,3,3] × [p] | |
| 5 | D4×I2(p) | [31,1,1] × [p] | |
| # | Coxeter group | Coxeter-Dynkin diagram | |
|---|---|---|---|
| 6 | A3×A3 | [3,3] × [3,3] | |
| 7 | A3×B3 | [3,3] × [4,3] | |
| 8 | A3×H3 | [3,3] × [5,3] | |
| 9 | B3×B3 | [4,3] × [4,3] | |
| 10 | B3×H3 | [4,3] × [5,3] | |
| 11 | H3×A3 | [5,3] × [5,3] | |
Uniform triprisms
There is one infinite family of uniform triaprismatic families of polytopes constructed as a Cartesian products of three regular polygons. Each combination of at least one ring on every connected group produces a uniform prismatic 6-polytope.
| # | Coxeter group | Coxeter-Dynkin diagram | |
|---|---|---|---|
| 1 | I2(p)×I2(q)×I2(r) | [p] × [q] × [r] | |
Rank 7[edit]
(7-space)
- A7: [3,3,3,3,3,3]












 (8-simplex)
(8-simplex) - B7: [4,3,3,3,3,3]












 (8-orthoplex/8-hypercube)
(8-orthoplex/8-hypercube) - D7: [34,1,1]










 (8-orthoplex)
(8-orthoplex) - E7: [33,2,1]










 (3_21 polytope)
(3_21 polytope)
There are 16 uniform prismatic families based on the uniform 6-polytopes.
| # | Coxeter group | Coxeter-Dynkin diagram | |
|---|---|---|---|
| 1 | A6×A1 | [35] × [ ] | |
| 2 | B6×A1 | [4,34] × [ ] | |
| 3 | D6×A1 | [33,1,1] × [ ] | |
| 4 | E6×A1 | [32,2,1] × [ ] | |
| 5 | A4×I2(p)×A1 | [3,3,3] × [p] × [ ] | |
| 6 | B4×I2(p)×A1 | [4,3,3] × [p] × [ ] | |
| 7 | F4×I2(p)×A1 | [3,4,3] × [p] × [ ] | |
| 8 | H4×I2(p)×A1 | [5,3,3] × [p] × [ ] | |
| 9 | D4×I2(p)×A1 | [31,1,1] × [p] × [ ] | |
| 10 | A3×A3×A1 | [3,3] × [3,3] × [ ] | |
| 11 | A3×B3×A1 | [3,3] × [4,3] × [ ] | |
| 12 | A3×H3×A1 | [3,3] × [5,3] × [ ] | |
| 13 | B3×B3×A1 | [4,3] × [4,3] × [ ] | |
| 14 | B3×H3×A1 | [4,3] × [5,3] × [ ] | |
| 15 | H3×A3×A1 | [5,3] × [5,3] × [ ] | |
| 16 | I2(p)×I2(q)×I2(r)×A1 | [p] × [q] × [r] × [ ] | |
There are 18 uniform duoprismatic forms based on Cartesian products of lower dimensional uniform polytopes.
| # | Coxeter group | Coxeter-Dynkin diagram | |
|---|---|---|---|
| 1 | A5×I2(p) | [3,3,3] × [p] | |
| 2 | B5×I2(p) | [4,3,3] × [p] | |
| 3 | D5×I2(p) | [32,1,1] × [p] | |
| 4 | A4×A3 | [3,3,3] × [3,3] | |
| 5 | A4×B3 | [3,3,3] × [4,3] | |
| 6 | A4×H3 | [3,3,3] × [5,3] | |
| 7 | B4×A3 | [4,3,3] × [3,3] | |
| 8 | B4×B3 | [4,3,3] × [4,3] | |
| 9 | B4×H3 | [4,3,3] × [5,3] | |
| 10 | H4×A3 | [5,3,3] × [3,3] | |
| 11 | H4×B3 | [5,3,3] × [4,3] | |
| 12 | H4×H3 | [5,3,3] × [5,3] | |
| 13 | F4×A3 | [3,4,3] × [3,3] | |
| 14 | F4×B3 | [3,4,3] × [4,3] | |
| 15 | F4×H3 | [3,4,3] × [5,3] | |
| 16 | D4×A3 | [31,1,1] × [3,3] | |
| 17 | D4×B3 | [31,1,1] × [4,3] | |
| 18 | D4×H3 | [31,1,1] × [5,3] | |
There are 3 uniform triaprismatic families based on Cartesian products of uniform polyhedrons and two regular polygons.
| # | Coxeter group | Coxeter-Dynkin diagram | |
|---|---|---|---|
| 1 | A3×I2(p)×I2(q) | [3,3] × [p] × [q] | |
| 2 | B3×I2(p)×I2(q) | [4,3] × [p] × [q] | |
| 3 | H3×I2(p)×I2(q) | [5,3] × [p] × [q] | |
Rank 8[edit]
(8-space)
- A8: [3,3,3,3,3,3,3]














 (8-simplex)
(8-simplex) - B8: [4,3,3,3,3,3,3]














 (8-orthoplex/8-hypercube)
(8-orthoplex/8-hypercube) - D8: [35,1,1]












 (8-orthoplex)
(8-orthoplex) - E8: [34,2,1]












 (4_21 polytope)
(4_21 polytope)
Four are based on the uniform 7-polytopes:
| # | Coxeter group | Coxeter-Dynkin diagram | |
|---|---|---|---|
| 1 | A7×A1 | [3,3,3,3,3,3] × [ ] | |
| 2 | B7×A1 | [4,3,3,3,3,3] × [ ] | |
| 3 | D7×A1 | [34,1,1] × [ ] | |
| 4 | E7×A1 | [33,2,1] × [ ] | |
Three are based on the uniform 6-polytopes and regular polygons:
| # | Coxeter group | Coxeter-Dynkin diagram | |
|---|---|---|---|
| 5 | A5×I2(p)×A1 | [3,3,3] × [p] × [ ] | |
| 6 | B5×I2(p)×A1 | [4,3,3] × [p] × [ ] | |
| 7 | D5×I2(p)×A1 | [32,1,1] × [p] × [ ] | |
Fifteen are based on the product of the uniform polychora and uniform polyhedra:
| # | Coxeter group | Coxeter-Dynkin diagram | |
|---|---|---|---|
| 8 | A4×A3×A1 | [3,3,3] × [3,3] × [ ] | |
| 9 | A4×B3×A1 | [3,3,3] × [4,3] × [ ] | |
| 10 | A4×H3×A1 | [3,3,3] × [5,3] × [ ] | |
| 11 | B4×A3×A1 | [4,3,3] × [3,3] × [ ] | |
| 12 | B4×B3×A1 | [4,3,3] × [4,3] × [ ] | |
| 13 | B4×H3×A1 | [4,3,3] × [5,3] × [ ] | |
| 14 | H4×A3×A1 | [5,3,3] × [3,3] × [ ] | |
| 15 | H4×B3×A1 | [5,3,3] × [4,3] × [ ] | |
| 16 | H4×H3×A1 | [5,3,3] × [5,3] × [ ] | |
| 17 | F4×A3×A1 | [3,4,3] × [3,3] × [ ] | |
| 18 | F4×B3×A1 | [3,4,3] × [4,3] × [ ] | |
| 19 | F4×H3×A1 | [3,4,3] × [5,3] × [ ] | |
| 20 | D4×A3×A1 | [31,1,1] × [3,3] × [ ] | |
| 21 | D4×B3×A1 | [31,1,1] × [4,3] × [ ] | |
| 22 | D4×H3×A1 | [31,1,1] × [5,3] × [ ] | |
Three are based on the uniform polyhedra and uniform duoprism:
| # | Coxeter group | Coxeter-Dynkin diagram | |
|---|---|---|---|
| 23 | A3×I2(p)×I2(q)×A1 | [3,3] × [p] × [q] × [ ] | |
| 24 | B3×I2(p)×I2(q)×A1 | [4,3] × [p] × [q] × [ ] | |
| 25 | H3×I2(p)×I2(q)×A1 | [5,3] × [p] × [q] × [ ] | |
There are 28 categorical uniform duoprismatic forms based on Cartesian products of lower dimensional uniform polytopes.
There are 4 based on the uniform 6-polytopes and regular polygons:
| # | Coxeter group | Coxeter-Dynkin diagram | |
|---|---|---|---|
| 1 | A6×I2(p) | [3,3,3,3,3] × [p] | |
| 2 | B6×I2(p) | [4,3,3,3,3] × [p] | |
| 3 | D6×I2(p) | [33,1,1] × [p] | |
| 4 | E6×I2(p) | [32,2,1] × [p] | |
There are 9 based on the uniform 5-polytopes and uniform polyhedra:
| # | Coxeter group | Coxeter-Dynkin diagram | |
|---|---|---|---|
| 5 | A5×A2 | [3,3,3,3] × [3,3] | |
| 6 | A5×B2 | [3,3,3,3] × [4,3] | |
| 7 | A5×H2 | [3,3,3,3] × [5,3] | |
| 8 | B5×A2 | [4,3,3,3] × [3,3] | |
| 9 | B5×B2 | [4,3,3,3] × [4,3] | |
| 10 | B5×H2 | [4,3,3,3] × [5,3] | |
| 11 | D5×A2 | [32,1,1] × [3,3] | |
| 12 | D5×B2 | [32,1,1] × [4,3] | |
| 13 | D5×H2 | [32,1,1] × [5,3] | |
Finally there are 20 based on two uniform 4-polytopes:
| # | Coxeter group | Coxeter-Dynkin diagram | |
|---|---|---|---|
| 14 | A4xA4 | [3,3,3] × [3,3,3] | |
| 15 | A4xB4 | [3,3,3] × [4,3,3] | |
| 16 | A4xD4 | [3,3,3] × [31,1,1] | |
| 17 | A4xF4 | [3,3,3] × [3,4,3] | |
| 18 | A4xH4 | [3,3,3] × [5,3,3] | |
| 19 | B4xB4 | [4,3,3] × [4,3,3] | |
| 20 | B4xD4 | [4,3,3] × [31,1,1] | |
| 21 | B4xF4 | [4,3,3] × [3,4,3] | |
| 22 | B4xH4 | [4,3,3] × [5,3,3] | |
| 23 | D4xD4 | [31,1,1] × [31,1,1] | |
| 24 | D4xF4 | [31,1,1] × [3,4,3] | |
| 25 | D4xH4 | [31,1,1] × [5,3,3] | |
| 26 | F4xF4 | [3,4,3] × [3,4,3] | |
| 27 | F4xH4 | [3,4,3] × [5,3,3] | |
| 28 | H4xH4 | [5,3,3] × [5,3,3] | |
There are 11 categorical uniform triaprismatic forms based on Cartesian products of lower dimensional uniform polytopes, for example these regular products:
Six are based on products of the uniform 4-polytopes and uniform duoprisms:
| # | Coxeter group | Coxeter-Dynkin diagram | |
|---|---|---|---|
| 1 | A4×I2(p)×I2(q) | [3,3,3] × [p] × [q] | |
| 2 | B4×I2(p)×I2(q) | [4,3,3] × [p] × [q] | |
| 3 | F4×I2(p)×I2(q) | [3,4,3] × [p] × [q] | |
| 4 | H4×I2(p)×I2(q) | [5,3,3] × [p] × [q] | |
| 5 | D4×I2(p)×I2(q) | [31,1,1] × [p] × [q] | |
| 6 | A3×A3×I2(p) | [3,3] × [3,3] × [p] | |
Five are based on triprism products of two uniform polyhedra and regular polygons:
| # | Coxeter group | Coxeter-Dynkin diagram | |
|---|---|---|---|
| 7 | A3×B3×I2(p) | [3,3] × [4,3] × [p] | |
| 8 | A3×H3×I2(p) | [3,3] × [5,3] × [p] | |
| 9 | B3×B3×I2(p) | [4,3] × [4,3] × [p] | |
| 10 | B3×H3×I2(p) | [4,3] × [5,3] × [p] | |
| 11 | H3×A3×I2(p) | [5,3] × [5,3] × [p] | |
There is one infinite family of uniform quadriprismatic figures based on Cartesian products of four regular polygons:
| # | Coxeter group | Coxeter-Dynkin diagram | |
|---|---|---|---|
| 1 | I2(p) x I2(q) x I2(r) x I2(s) | [p] x [q] x [r] x [s] | |
Rank 9[edit]
(9-space)
- A9: [3,3,3,3,3,3,3,3]
















 (9-simplex)
(9-simplex) - B9: [4,3,3,3,3,3,3,3]
















 (9-orthoplex/9-hypercube)
(9-orthoplex/9-hypercube) - D9: [36,1,1]














 (9-orthoplex)
(9-orthoplex)
Rank 10[edit]
(10-space)
Euclidean compact[edit]
Rank 2[edit]
(1-space)
- I~1: [∞]


 (apeirogon)
(apeirogon)
Rank 3[edit]
(2-space)
- A~2: (3 3 3)
 (triangular tiling)
(triangular tiling) - B~2: [4,4]




 (square tiling)
(square tiling) - H~2: [6,3]




 (triangular tiling/hexagonal tiling)
(triangular tiling/hexagonal tiling)
Rank 4[edit]
(3-space)
- A~3: (3 3 3 3)


 (quarter cubic honeycomb)
(quarter cubic honeycomb) - B~2: [4,3,4]






 (cubic honeycomb)
(cubic honeycomb) - D~3: [4,31,1]



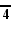
 (Alternated cubic honeycomb)
(Alternated cubic honeycomb)
(2-space prismatic)
- I~1xI~1: [∞]x[∞]






 =
= 



 (square tiling)
(square tiling)
Rank 5[edit]
(4-space)
- A~4: (3 3 3 3 3)



- B~4: [4,3,3,4]








 (Tesseractic honeycomb)
(Tesseractic honeycomb) - C~4: [4,3,31,1]





 (Demitesseractic honeycomb)
(Demitesseractic honeycomb) - D~4: [31,1,1,1]




 (Demitesseractic honeycomb)
(Demitesseractic honeycomb) - F~4: [3,4,3,3]








 (Icositetrachoric honeycomb/Demitesseractic honeycomb)
(Icositetrachoric honeycomb/Demitesseractic honeycomb)
(3-space prismatic)
Rank 6[edit]
(5-space)
(4-space prismatic)
- I~1xI~1xI2r: [∞] x [∞] x [r] = [4,4]x[r] -










 =
= 








- B~3xI~1: [4,3,4]x[∞]











- D~3xI~1: [4,31,1]x[∞]







- A~3xI~1:






- A~2xA~2: [Δ]x[Δ]



- A~2xB~2: [Δ]x[4,4]







- A~2xH~2: [Δ]x[6,3]







- B~2xB~2: [4,4]x[4,4]











- B~2xH~2: [4,4]x[6,3]











- H~2xH~2: [6,3]x[6,3]











- A4xI~1: [3,3,3]x[∞]










 (5-cell column)
(5-cell column) - B4xI~1: [4,3,3]x[∞]










 (tesseract/16-cell column)
(tesseract/16-cell column) - H4xI~1: [5,3,3]x[∞]

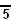








 (120-cell/600-cell column)
(120-cell/600-cell column) - F4xI~1: [3,4,3]x[∞]










 (24-cell column)
(24-cell column) - D4xI~1: [31,1,1]x[∞]








 (24-cell column)
(24-cell column)
(3-space prismatic)
Rank 7[edit]
(6-space)
(6-space prismatic)
- A5xI~1: [3,3,3] x [∞]













- B5xI~1: [4,3,3] x [∞]













- D5xI~1: [32,1,1] x [∞]









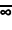

- A4xI~1xA1: [3,3,3] x [∞] x [ ]













- B4xI~1xA1: [4,3,3] x [∞] x [ ]













- F4xI~1xA1: [3,4,3] x [∞] x [ ]













- H4xI~1xA1: [5,3,3] x [∞] x [ ]

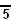











- D4xI~1xA1: [31,1,1] x [∞] x [ ]











- A3xI~1xI2q: [3,3] x [∞] x [q]











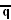

- B3xI~1xI2q: [4,3] x [∞] x [q]











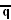

- H3xI~1xI2q: [5,3] x [∞] x [q]

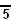









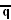

- I~1xI2qxI2rA1: [∞] x [q] x [r] x [ ]





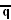







(5-space prismatic)
- A3xI~1xI~1: [3,3] x [∞] x [∞]













- B3xI~1xI~1: [4,3] x [∞] x [∞]













- H3xI~1xI~1: [5,3] x [∞] x [∞]

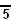











- I~1xI~1xI2rxA1: [∞] x [∞] x [r] x [ ]













(4-space prismatic)
Rank 8[edit]
(7-space)
Rank 9[edit]
(8-space)
- A~9: (3 3 3 3 3 3 3 3)







- B~8: [4,3,3,3,3,3,3,4]

















- C~8: [4,34,31,1]

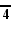













- D~8: [31,1,34,31,1]













- E~8: [35,2,1]














 (E8 lattice)
(E8 lattice)
Rank 10[edit]
(9-space)
Euclidean noncompact[edit]
Rank 3[edit]
(2-space)
- I~1xA1: [∞]x[ ]




 (apeirogonal prism)
(apeirogonal prism)
Rank 4[edit]
(3-space)
- B~2xA1: [4,4]x[ ]






 (cubic prismatic slab)
(cubic prismatic slab) - H~2xA1: [6,3]x[ ]






 (triangular/hexagonal prismatic slab)
(triangular/hexagonal prismatic slab) - A~2xA1: (3 3 3 3)x[ ]


 (triangular prismatic slab)
(triangular prismatic slab) - I~1xA1xA1: [∞]x[ ]x[ ]






 =
= 





 (4-∞ semi-infinite duoprism)
(4-∞ semi-infinite duoprism) - I2(p)xI~1: [p]x[∞]

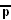




 (p-∞ semiinfinite duoprism)
(p-∞ semiinfinite duoprism)
Rank 5[edit]
(4-space)
- I2pxI~1xA1: [p]x[∞]x[ ] -

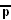







- D~3xA1: [4,31,1]x[ ]



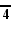



- A~3xA1: (3 3 3 3)x[ ]





- A~2xI2p: (3 3 3)x[p]



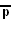

- B~2xI2p: [4,4]x[p]







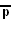

- H~2xI2p: [6,3]x[p]







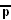

(3-space)
- I~1xI~1xA1: [∞]x[∞]x[ ] -









- B~2xI2p: [4,4]x[∞]









- H~2xI2p: [6,3]x[∞]







- A~2xI2pxA1: [Δ]x[∞]x[ ]



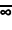

- B~2xA1: [4,3,4]x[ ]









Rank 6[edit]
(5-space)
- A4xI~1: [3,3,3]x[∞] -











- B4xI~1: [4,3,3]x[∞] -











- F4xI~1: [3,4,3]x[∞] -











- H4xI~1: [5,3,3]x[∞] -

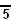









- D4xI~1: [31,1,1] x [∞] -







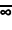

- A3xI~1xA1: [3,3] x [∞] x [ ] -











- B3xI~1xA1: [4,3] x [∞] x [ ] -











- H3xI~1xA1: [5,3] x [∞] x [ ] -

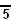









- I~1xI2qxI2r: [∞] x [q] x [r] -





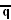





- A~4xA1: (3 3 3 3)x[ ]





- B~4xA1: [4,3,3,4]x[ ]











- C~4xA1: [4,3,31,1]x[ ]

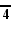







- D~4xA1: [31,1,1,1]x[ ]







- F~4xA1: [3,4,3,3]x[ ]











Rank 7[edit]
Rank 8[edit]
Rank 9[edit]
Rank 10[edit]
Hyperbolic compact[edit]
Rank 3[edit]
(2-space)
Rank 4[edit]
(3-space)
- [3,5,3]



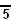


 (Order-3 icosahedral honeycomb)
(Order-3 icosahedral honeycomb) - [5,3,4]

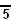




 (Order-5 cubic honeycomb/Order-4 dodecahedral honeycomb)
(Order-5 cubic honeycomb/Order-4 dodecahedral honeycomb) - [5,3,5]

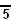



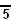
 (Order-5 dodecahedral honeycomb)
(Order-5 dodecahedral honeycomb) - [5,31,1]

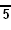



- (4 3 3 3)
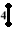


- (5 3 3 3)



- (4 3 3 3)
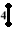


- (4 3 5 3)
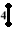

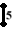
- (5 3 5 3)


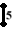
(2-space)
Rank 5[edit]
(4-space)
- [5,3,3,3]

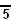






 (Order-5 pentachoronic tetracomb/Order-3 hecatonicosachoronic tetracomb)
(Order-5 pentachoronic tetracomb/Order-3 hecatonicosachoronic tetracomb) - [5,3,3,4]

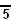






 (Order-5 tesseractic tetracomb/Order-4 hecatonicosachoronic tetracomb)
(Order-5 tesseractic tetracomb/Order-4 hecatonicosachoronic tetracomb) - [5,3,3,5]

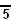





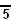
 (Order-5 hecatonicosachoronic tetracomb)
(Order-5 hecatonicosachoronic tetracomb) - [5,3,31,1]

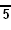




 (Order-5 demitesseractic tetracomb)
(Order-5 demitesseractic tetracomb) - (4 3 3 3 3)













Rank 6[edit]
Noncompact!
(5-space)
Rank 7[edit]
Rank 8[edit]
Rank 9[edit]
Rank 10[edit]
Hyperbolic noncompact[edit]
Rank 3[edit]
(2-space)
Rank 4[edit]
(3-space)
Rank 5[edit]
(4-space)
Rank 6[edit]
Rank 7[edit]
Rank 8[edit]
Rank 9[edit]
Rank 10[edit]
Finite Coexter groups[edit]
| Group symbol |
Alternate symbol |
Rank | Order | Related polytopes | Coxeter-Dynkin diagram |
|---|---|---|---|---|---|
| An | An | n | (n + 1)! | n-simplex | |
| Bn = Cn | Cn | n | 2n n! | n-hypercube / n-cross-polytope | |
| Dn | Bn | n | 2n−1 n! | demihypercube | |
| I2(p) | D2p | 2 | 2p | p-gon | |
| H3 | G3 | 3 | 120 | icosahedron / dodecahedron | |
| F4 | F4 | 4 | 1152 | 24-cell | |
| H4 | G4 | 4 | 14400 | 120-cell / 600-cell | |
| E6 | E6 | 6 | 51840 | 122 polytope | |
| E7 | E7 | 7 | 2903040 | 321 polytope | |
| E8 | E8 | 8 | 696729600 | E8 polytope |
Finite Coxeter groups[edit]
Families of convex uniform polytopes are defined by Coxeter groups.
Note: (Alternate names as Simple Lie groups also given)
- An forms the simplex polytope family. (Same An)
- Bn is the family of demihypercubes, beginning at n=4 with the 16-cell, and n=5 with the demipenteract. (Also named Dn)
- Cn forms the hypercube polytope family. (Same Cn)
- D2n forms the regular polygons. (Also named I1n)
- E6,E7,E8 are the generators of the Gosset Semiregular polytopes (Same E6,E7,E8)
- F4 is the 24-cell polychoron family. (Same F4)
- G3 is the dodecahedron/icosahedron polyhedron family. (Also named H3)
- G4 is the 120-cell/600-cell polychoron family. (Also named H4)
Affine Coxeter groups (Euclidean)[edit]
| Group symbol |
Alternate symbol |
Related uniform tessellation(s) | Coxeter-Dynkin diagram |
|---|---|---|---|
| A~n-1 | Pn | Simplex-rectified-simplex honeycomb A~2:Triangular tiling A~3:Tetrahedral-octahedral honeycomb |
|
| B~n-1 | Rn | Hypercubic honeycomb | |
| C~n-1 | Sn | Demihypercubic honeycomb | |
| D~n-1 | Qn | Demihypercubic honeycomb | |
| I~1 | W2 | apeirogon | |
| H~2 | G3 | Hexagonal tiling and Triangular tiling |
|
| F~4 | V5 | Hexadecachoric tetracomb and Icositetrachoronic tetracomb or F4 lattice |
|
| E~6 | T7 | E6 lattice | |
| E~7 | T8 | E7 lattice | |
| E~8 | T9 | E8 lattice |
| n | A~2+ (3n) |
D~4+ [31,1,3n-5,31,1] |
B~2+ [4,3n-3,4] |
C~3+ [4,3n-4,31,1] |
E~6-8 [3a,b,c] |
F~4 [3,4,3,3] |
H~2 [6,3] |
I~1 |
|---|---|---|---|---|---|---|---|---|
| 2 | I~1=[∞] | |||||||
| 3 | A~2=h[6,3] | B~2=[4,4] | F~2=[6,3] | |||||
| 4 | A~3=q[4,3,4] | B~3=[4,3,4] | C~3=h[4,3,4] | |||||
| 5 | A~4 | D~4=q[4,32,4] | B~4=[4,32,4] | C~4=h[4,32,4] | U5=[3,4,3,3] | |||
| 6 | A~5 | D~5=q[4,33,4] | B~5=[4,33,4] | C~5=h[4,33,4] | ||||
| 7 | A~6 | D~6=q[4,34,4] | B~6=[4,34,4] | C~6=h[4,34,4] | E~6=[32,2,2] | |||
| 8 | A~7 | D~7=q[4,35,4] | B~7=[4,35,4] | C~7=h[4,35,4] | E~7=[33,3,1] | |||
| 9 | A~8 | D~8=q[4,36,4] | B~8=[4,36,4] | C~8=h[4,36,4] | E~8=[35,2,1] | |||
| 10 | A~9 | D~9=q[4,37,4] | B~9=[4,37,4] | C~9=h[4,37,4] | ||||
| 11 | ... | ... | ... | ... |
See also[edit]
References[edit]
- THE GROWTH SERIES OF COMPACT HYPERBOLIC COXETER GROUPS WITH 4 AND 5 GENERATORS
- Spacelike Singularities and Hidden Symmetries of Gravity: 3 Hyperbolic Coxeter Groups
- Reflection Groups and Coxeter groups (Cambridge studies in advanced mathematics 29) , James E. Humphreys, Cambridge University press, 1990 ISBN 0521436133 (paperback), ISBN 052137510X (hardcopy)
- 2.4 Some positive definite graphs, 2.5 Some positive semidefinite graphs, 6.8 Coxeter Hyperbolic groups
